Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập ôn tập cuối chương V SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Phát biểu nào sau đây sai?
Giá trị của limn−22n2+6 bằng
Cho hình vuông ABCD có cạnh bằng a1 và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2, B2, C2, D2 có diện tích S3, …và cứ tiếp tục làm như thế.

Giả sử quá trình trên kéo dài vô hạn. Tính tổng diện tích (đơn vị cm2) các hình vuông được tạo thành biết a1=4 cm.
Trả lời:
Giá trị của x→1lim(2x2−3x+1) bằng
x→(−3)−limx2+6x+9x+3 bằng
Giới hạn x→+∞lim(x2−x−3x3+1) bằng bao nhiêu? (làm tròn đến chữ số hàng phần mười)
Trả lời:
Cho hàm số f(x)=x−ax3.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Khi a=0, x→+∞limf(x)=+∞. |
|
| b) Khi a=0, x→−∞limf(x)=−∞. |
|
| c) Khi a>0, x→+∞limf(x)=+∞. |
|
| d) Có tất cả 2025 giá trị nguyên a thuộc [−2024;2025] để x→+∞limf(x)=+∞. |
|
Cho các hàm số f1(x)=x3; f2(x)=2x−1; f3(x)=⎩⎨⎧x−3x2−2x−3khix=35khix=3. Hàm số nào không liên tục tại điểm x0=3?
Cho hàm số y=f(x)=⎩⎨⎧x2+x+1khix≤−1x+2khi−1<x<12x+3khix≥1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số y=f(x) liên tục tại điểm x=−2. |
|
| b) Hàm số y=f(x) không liên tục tại điểm x=0. |
|
| c) Hàm số y=f(x) liên tục tại điểm x=−1. |
|
| d) Hàm số y=f(x) liên tục tại điểm x=1. |
|
Cho hàm số y=f(x)={x2−3x+1khix=−1mxkhix=−1. Giá trị của m để hàm số liên tục trên R là
Cho các hàm số f(x)=x−12x2−x−1, g(x)=x+15 và h(x)={f(x)khix<1g(x)khix≥1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số f(x) liên tục trên khoảng (−∞;1). |
|
| b) Hàm số g(x) liên tục trên khoảng (1;+∞). |
|
| c) h(1)=4. |
|
| d) Hàm số h(x) liên tục trên R. |
|
Hàm số v(t)={−t2+4t+12khi0≤t≤5at−3khi5<t≤10 mô tả vận tốc (m/s) của một vật tại thời điểm t (giây) trong khoảng thời gian 10 giây đầu tiên kể từ khi vật bắt đầu chuyển động. Biết rằng y=v(t) là hàm liên tục trên đoạn [0;10] và trong 10 giây đầu tiên đó, có hai lần vật đạt vận tốc 10 m/s là vào các thời điểm t1 giây và t2 giây. Tính t1+t2 (Kết quả làm tròn đến hàng phần mười)
Trả lời:
Một bãi đỗ xe tính phí 60 000 đồng cho giờ đầu tiên (hoặc một phần của giờ đầu tiên) và thêm 40 000 đồng cho mỗi giờ (hoặc một phần của mỗi giờ) tiếp theo, tối đa là 200 000 đồng.
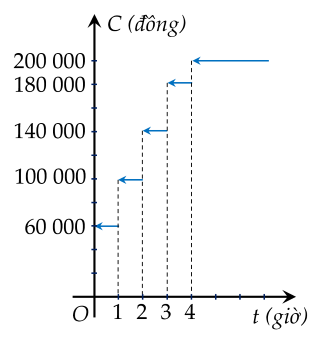
| a) Đồ thị hàm số C=C(t) biểu thị chi phí theo thời gian đỗ xe. |
|
| b) Hàm số C=C(t) liên tục trên [0;+∞). |
|
| c) Từ đồ thị ta thấy t→3limC(t)=180000. |
|
| d) Một người có thời gian đỗ xe tăng dần đến 3 giờ và một người có thời gian đỗ xe giảm dần đến 3 giờ thì chênh lệch chi phí giữa hai người là 20000 đồng. |
|
