olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Ôn tập và kiểm tra chương Hàm số và phương trình lượng giác SVIP

Tải ma trận In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Với góc xx bất kì, khẳng định nào sau đây đúng?

sin⁡2x+cos⁡22x=1\sin^2 x+ \cos^2 2x=1.
sin⁡2x+cos⁡2(180∘−x)=1\sin^2 x+\cos^2 \left(180^\circ -x\right)=1.
sin⁡2x−cos⁡2(180∘−x)=1\sin^2 x-\cos^2 \left(180^\circ -x \right)=1.
sin⁡(x2)+cos⁡(x2)=1\sin (x^2) + \cos (x^2)=1.
Câu 2 (1đ):

Cho sin⁡a=13\sin a=\dfrac{1}{3}. Giá trị của biểu thức A=cot⁡a−tan⁡atan⁡a+2cot⁡aA=\dfrac{\cot a-\tan a}{\tan a+2\cot a} bằng

717\dfrac{7}{17}.
1781\dfrac{17}{81}.
19\dfrac{1}{9}.
79\dfrac{7}{9}.
Câu 3 (1đ):
Câu 4 (1đ):

Xét hàm số y=sin⁡xy=\sin x trên khoảng (−π ; π)\left(-\pi \,;\,\pi \right). Đồ thị của hàm số có hướng đi xuống trên khoảng

(−π2 ; π2)\Big(-\dfrac{\pi }{2}\,;\,\dfrac{\pi }{2} \Big).
(−π ; 0)\left(-\pi \,;\,0 \right).
(π2 ; π)\Big(\dfrac{\pi }{2}\,;\,\pi \Big).
(0 ; π)\left(0\,;\,\pi \right).
Câu 5 (1đ):

Hàm số y=sin⁡xy=\sin x đồng biến trên khoảng nào dưới đây?

(π;2π)\left(\pi ;2\pi \right).
(π2;π)\Big(\dfrac{\pi }{2};\pi \Big).
(3π2;2π)\Big(\dfrac{3\pi }{2};2\pi \Big).
(π2;3π2)\Big(\dfrac{\pi }{2};\dfrac{3\pi }{2} \Big).
Câu 6 (1đ):

Phương trình lượng giác cos⁡3x=cos⁡π15\cos 3x=\cos \dfrac{\pi }{15} có nghiệm là

x=π45+k2π3, k∈Zx=\dfrac{\pi }{45}+\dfrac{k2\pi }{3},\,k\in \mathbb{Z}.
x=±π45+k2π3, k∈Zx=\pm \dfrac{\pi }{45}+\dfrac{k2\pi }{3},\,k\in \mathbb{Z}.
x=±π15+k2π, k∈Zx=\pm \dfrac{\pi }{15}+k2\pi, \, k\in \mathbb{Z}.
x=−π45+k2π3, k∈Zx=\dfrac{-\pi }{45}+\dfrac{k2\pi }{3},\,k\in \mathbb{Z}.
Câu 7 (1đ):

Phương trình cos⁡x=−32\cos x=-\dfrac{\sqrt{3}}{2} có tập nghiệm là

{x=±π6+kπ ∣ k∈Z}\Big\{ x=\pm \dfrac{\pi }{6}+k\pi \, \Big| \, k\in \mathbb{Z} \Big\}.
{x=±π3+kπ ∣ k∈Z}\Big\{ x=\pm \dfrac{\pi }{3}+k\pi \, \Big| \,k\in \mathbb{Z} \Big\}.
{x=±5π6+k2π ∣ k∈Z}\Big\{ x=\pm \dfrac{5\pi }{6}+k2\pi\, \Big| \, k\in \mathbb{Z} \Big\}.
{x=±π3+k2π ∣ k∈Z}\Big\{ x=\pm \dfrac{\pi }{3}+k2\pi \, \Big| \, k\in \mathbb{Z} \Big\}.
Câu 8 (1đ):

Với x, yx,\,y là hai góc nhọn, dương và tan⁡x=3tan⁡y\tan x=3\tan y thì hiệu số x−yx-y sẽ

lớn hơn hoặc bằng 45∘45^\circ.
nhỏ hơn hoặc bằng 30∘30^\circ.
lớn hơn hoặc 30∘30^\circ.
nhỏ hơn hoặc bằng 45∘45^\circ.
Câu 9 (1đ):

Tập xác định của hàm số y=tan⁡x1−tan⁡xy=\dfrac{\tan x}{1-\tan x} là

D=R\{π2+kπ; π4+kπ ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ; \, \dfrac{\pi }{4}+k\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{−π2+k2π; −π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ -\dfrac{\pi }{2}+k2\pi ; \, -\dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{π2+kπ; π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi ; \, \dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
D=R\{π2+k2π; π4+k2π ∣ k∈Z}D=\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi ; \, \dfrac{\pi }{4}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
Câu 10 (1đ):

Hàm số nào sau đây là hàm số chẵn?

y=tan⁡x2.y=\tan \dfrac{x}{2}.
y=sin⁡3x.y=\sin 3x.
y=sin⁡x.cos⁡x.y=\sin x.\cos x.
y=sin⁡2x.cos⁡x.y=\sin^2 x.\cos x.
Câu 11 (1đ):

Trên khoảng (π2;2π)\Big(\dfrac{\pi }{2};2\pi \Big), phương trình cos⁡(π6−2x)=sin⁡x\cos \Big(\dfrac{\pi }{6}-2x \Big)=\sin x có bao nhiêu nghiệm?

55.
44.
33.
22.
Câu 12 (1đ):

Có bao nhiêu giá trị nguyên của tham số mm thuộc đoạn [−2 018;2 018]\left[ -2 \,018;2 \,018 \right] để phương trình mcos⁡x+1=0m\cos x+1=0 có nghiệm?

2 0182 \, 018.
4 0374 \, 037.
2 0192 \, 019.
4 0364 \, 036.
Câu 13 (1đ):

Cho góc lượng giác α\alpha thỏa mãn 0<α<π20<\alpha <\dfrac{\pi }{2}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) cos⁡(α+π)<0\cos (\alpha +\pi)<0.
b) tan⁡(α−π)>0\tan (\alpha -\pi)>0.
c) sin⁡(α+2π5)<0\sin \Big(\alpha +\dfrac{2\pi }{5} \Big)<0.
d) cos⁡(α−3π8)<0\cos \Big(\alpha -\dfrac{3\pi }{8} \Big)<0.
Câu 14 (1đ):

Cho hàm số f(x)=tan⁡xf(x)=\tan x và g(x)=cot⁡2x−sin⁡2x2g(x)=\cot^2 x-\dfrac{\sin 2x}{2}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Tập xác định hàm số f(x)f(x) là D=R\{π2+kπ ∣ k∈Z}D=\mathbb{R}\backslash \Big\{ \dfrac{\pi }{2}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
b) Hàm số f(x)f(x) là hàm số không tuần hoàn.
c) Tập xác định hàm số g(x)g(x) là D=R\{kπ ∣ k∈Z}D=\mathbb{R}\backslash \{k\pi \, \big| \, k\in \mathbb{Z}\}.
d) Hàm số g(x)g(x) là hàm số tuần hoàn.
Câu 15 (1đ):

Một vật dao động xung quanh vị trí cân bằng theo phương trình x=1,5cos⁡(tπ4)x=1,5\cos \Big(\dfrac{t\pi }{4}\Big); trong đó tt là thời gian được tính bằng giây và quãng đường h=∣x∣h=|x| được tính bằng mét là khoảng cách theo phương ngang của vật đối với vị trí cân bằng.

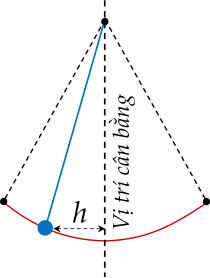
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Vật ở xa vị trí cân bằng nhất nghĩa là h=1,5h=1,5 m.
b) Trong 1010 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì cos⁡(tπ4)=0\cos \Big( \dfrac{t\pi }{4} \Big)=0.
d) Trong khoảng từ 00 đến 2020 giây thì vật đi qua vị trí cân bằng 44 lần.
Câu 16 (1đ):

Cho phương trình lượng giác cot⁡3x=−13\cot 3x=-\dfrac{1}{\sqrt{3}} (*).

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Phương trình (*) tương đương cot⁡3x=cot⁡(−π6)\cot 3x=\cot \Big(\dfrac{-\pi }{6} \Big).
b) Phương trình (*) có nghiệm x=π9+kπ3, (k∈Z)x=\dfrac{\pi }{9}+k\dfrac{\pi }{3}, \, (k\in \mathbb{Z}).
c) Tổng các nghiệm của phương trình trong khoảng (−π2;0)\left(-\dfrac{\pi }{2};0 \right) bằng −5π9\dfrac{-5\pi }{9}.
d) Phương trình có nghiệm dương nhỏ nhất bằng 2π9\dfrac{2\pi }{9}.
Câu 17 (1đ):

Một chiếc đu quay có bán kính 7575 m, tâm của vòng quay ở độ cao 9090 m, thời gian thực hiện mỗi vòng quay của đu quay là 3030 phút.

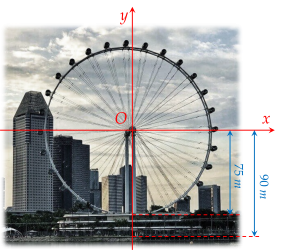
loading...

Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 2020 phút quay, người đó ở độ cao bao nhiêu mét? (làm tròn kết quả tới hàng phần mười)

Trả lời:

Câu 18 (1đ):

Hàm số y=sin⁡(x+π3)−sin⁡xy=\sin \Big(x+\dfrac{\pi }{3} \Big)-\sin x có bao nhiêu giá trị nguyên?

Trả lời:

Câu 19 (1đ):

Tìm số nghiệm của phương trình tan⁡3x−tan⁡x=0\tan 3x-\tan x=0 trên nửa khoảng [0;2π)\left[ 0;2\pi \right).

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP