Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập chủ đề 1 SVIP
Bài 1. Cho hai vật dao động điều hòa (1) và (2) có đồ thị li độ - thời gian như Hình 1.
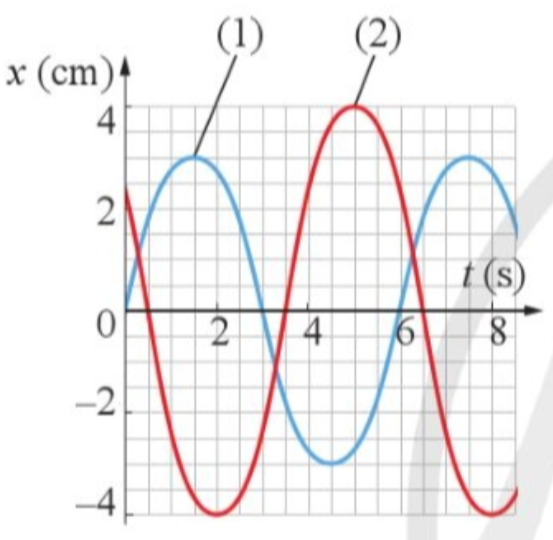
Hình 1
a. Xác định biên độ, chu kì và tần số của hai dao động.
b. Xác định độ lệch pha của hai dao động ra đơn vị độ và rad.
c. Tìm vận tốc của vật (2) tại thời điểm 3,5 s.
d. Tìm gia tốc của vật (1) tại thời điểm 1,5 s.
Hướng dẫn giải:
a. Xét dao động (1) có:
- Biên độ: \(A_1=3\) cm
- Chu kì: \(T_1=6\) s
- Tần số: \(f_1=\dfrac{1}{T_1}=\dfrac{1}{6}\) Hz
Xét dao động (2) có:
- Biên độ: \(A_2=4\) cm
- Chu kì: \(T_2=6\) s
- Tần số: \(f_2=\dfrac{1}{T_2}=\dfrac{1}{6}\) Hz
b. Nhận xét: ta thấy tại thời điểm \(t_1=2\) s thì vật (2) tới vị trí biên âm, sau đó đến thời điểm \(t_2=4,5\) s thì vật (1) tới vị trí biên âm.
Độ lệch thời gian của hai dao động là: \(\Delta t=t_2-t_1=2,5\) s
Hai dao động có cùng tần số góc là: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\) rad/s
Độ lệch pha của hai dao động là: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}.2,5=\dfrac{5\pi}{6}\) rad \(=150^o\)
c. Tại thời điểm 3,5 s thì vật (2) đang ở vị trí cân bằng nên vận tốc của vật có độ lớn cực đại: \(\text{v}=\left|\text{v}_{max}\right|=\omega A_2=\dfrac{\pi}{3}.4=\dfrac{4\pi}{3}\) cm/s
Và thời điểm đó vật chuyển động cùng chiều dương của trục Ox nên vận tốc của vật có giá trị dương, suy ra vận tốc của vật khi đó là: \(\text{v}=\dfrac{4\pi}{3}\) cm/s
d. Tại thời điểm 1,5 s thì vật (1) đang ở vị trí biên dương, gia tốc của vật khi đó là:
\(a=-\omega^2x=-\omega^2A_1=-\left(\dfrac{\pi}{3}\right)^2.3=-3,29\) cm/s2
Bài 2. Cho con lắc lò xo dao động trên mặt phẳng nằm ngang không ma sát như trong Hình 2. Con lắc lò xo thực hiện mỗi dao động mất 2,4 s. Tại $t=0$, vật bắt đầu dao động với vận tốc bằng không từ vị trí cách vị trí cân bằng $x=3$ cm.
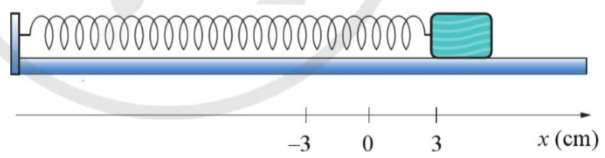
Hình 2
a. Tìm vị trí và vận tốc của vật tại thời điểm 0,60 s.
b. Tìm vị trí và vận tốc của vật tại thời điểm 1,20 s.
Hướng dẫn giải:
Con lắc lò xo thực hiện mỗi dao động mất 2,4 s \(\Rightarrow T=2,4\) s
\(\omega=\dfrac{2\pi}{T}=\dfrac{5\pi}{6}\) rad/s
Tại $t=0$, vật bắt đầu dao động với vận tốc bằng không từ vị trí cách vị trí cân bằng $x=3$ cm \(\Rightarrow A=3\) cm
Tại thời điểm ban đầu ta có: \(3=3\cos\varphi\Rightarrow\varphi=0\) rad
Khi đó phương trình li độ có dạng: \(x=3\cos\left(\dfrac{5\pi}{6}t\right)\) cm
Phương trình vận tốc có dạng: \(\text{v}=-\dfrac{5\pi}{6}.3.\sin\left(\dfrac{5\pi}{6}t\right)=-\dfrac{5\pi}{2}.\sin\left(\dfrac{5\pi}{6}t\right)\) cm/s
a. Tại thời điểm $t=0,6$ s:
\(x=3\cos\left(\dfrac{5\pi}{6}.0,6\right)=0\) cm
\(\text{v}=-\dfrac{5\pi}{2}.\sin\left(\dfrac{5\pi}{6}.0,6\right)=-\dfrac{5\pi}{2}\) cm/s
b. Tại thời điểm $t=1,2$ s:
\(x=3\cos\left(\dfrac{5\pi}{6}.1,2\right)=-3\) cm
\(\text{v}=-\dfrac{5\pi}{2}.\sin\left(\dfrac{5\pi}{6}.1,2\right)=0\) cm/s
Bài 3. Trong một chuyến bay lên Mặt Trăng, các nhà du hành đã mang theo một con lắc đơn với dây treo có chiều dài 1,6 m. Phép đo chu kì dao động của con lắc đơn này trên Mặt Trăng cho kết quả $T$ = 6,2 s. Xác định gia tốc rơi tự do tại bề mặt Mặt Trăng.
Hướng dẫn giải:
\(T=2\pi\sqrt{\dfrac{l}{g}}\Rightarrow g=\dfrac{4\pi^2.l}{T^2}=\dfrac{4\pi^2.1,6}{6,2^2}=1,64\) m/s2
Bài 4. Cho đồ thị vận tốc - thời gian của một vật dao động điều hòa như Hình 3. Biết rằng khối lượng của vật là 0,15 kg. Hãy xác định:
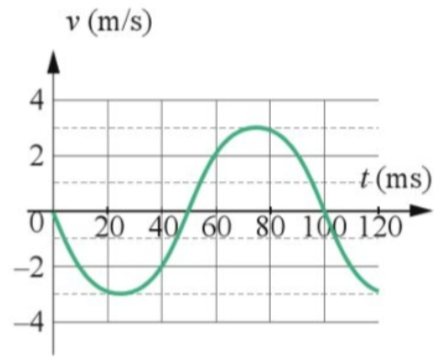
Hình 3
a. Chu kì của vật dao động.
b. Biên độ của vật dao động.
c. Cơ năng của vật dao động.
d. Vị trí và gia tốc của vật tại thời điểm 100 ms.
Hướng dẫn giải:
a. Chu kì: \(T=100ms=0,1s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{0,1}=20\pi\) rad/s
b. Từ đồ thị ta thấy vận tốc có độ lớn cực đại: \(\text{v}_{max}=3\) m/s
Suy ra biên độ của vật dao động là: \(A=\dfrac{\text{v}_{max}}{\omega}=\dfrac{3}{20\pi}=0,048\) m \(=4,8\) cm
c. Cơ năng của vật dao động:
\(W=W_{đmax}=\dfrac{1}{2}\text{mv}_{max}^2=\dfrac{1}{2}.0,15.3^2=0,675\) J
d. Tại thời điểm 100 ms, vật có vận tốc bằng 0 và đang đi theo chiều âm nên vị trí của vật là tại biên dương.
Gia tốc khi đó là: \(a=-\omega^2A=-\left(20\pi\right)^2.0,048=-189,5\) m/s2
Bài 5. Dao động của vật sẽ tắt dần nhanh hơn nếu
A. giảm lực ma sát.
B. tăng lực cản của môi trường.
C. tăng ngoại lực cưỡng bức tuần hoàn.
D. đặt vật dao động trong môi trường chân không.
Hướng dẫn giải:
Đáp án B.
Nguyên nhân làm dao động của vật tắt dần là do lực ma sát và lực cản của môi trường. Khi tăng lực ma sát và lực cản của môi trường thì dao động sẽ tắt dần nhanh hơn.
Bài 6. Phát biểu nào sau đây là sai khi nói về năng lượng của hệ dao động điều hòa?
A. Hệ có thế năng cực đại khi vật ở vị trí biên dương.
B. Vật có động năng cực đại khi ở vị trí cân bằng.
C. Hệ có cơ năng không đổi trong suốt quá trình dao động.
D. Hệ có thế năng bằng không khi vật ở vị trí biên âm.
Hướng dẫn giải:
Đáp án D.
Tại vị trí cân bằng, động năng của vật có độ lớn cực đại, thế năng của vật bằng 0.
Tại vị trí hai biên, động năng của vật bằng 0, thế năng có độ lớn cực đại.
Bài 7. Gờ giảm tốc có tác dụng cảnh báo (thông qua việc gây ra tác động nhẹ lên phương tiện) cho người tham gia giao thông biết trước đoạn đường nguy hiểm, cần phải giảm tốc độ và chú ý quan sát để bảo đảm an toàn giao thông.

Hình 4. Gờ giảm tốc
Một ô tô có khối lượng 1465 kg chở hai người có tổng khối lượng 110 kg đi qua một đoạn đường có gờ giảm tốc, với những nếp gấp cách nhau 0,50 m. Ô tô nảy lên với biên độ cực đại khi tốc độ của nó là 20 km/h. Xác định độ cứng tương đương của hệ thống lò xo gắn với khung xe. Cho rằng hệ thống này dao động như con lắc lò xo có chu kì dao động tính bằng công thức:
\(T=2\pi\sqrt{\dfrac{m}{k}}\)
Hướng dẫn giải:
Khoảng cách giữa nếp gấp của các gờ giảm tốc là 0,5 m, ô tô nảy lên với biên độ cực đại khi tốc độ của nó là 20 km/h, do đó chu kì là:
\(T=\dfrac{s}{v}=\dfrac{0,5}{\left(\dfrac{20}{3,6}\right)}=0,09s\)
Mặt khác: \(T=2\pi\sqrt{\dfrac{m}{k}}\Rightarrow k=\dfrac{4\pi^2m}{T^2}=\dfrac{4\pi^2.\left(1465+110\right)}{0,09^2}=7676359\) N/m
Bài 8. Các cơ vận động nhãn cầu tạo ra chuyển động của nhãn cầu và chuyển động đồng bộ của mi mắt. Các cơ giữ nhãn cầu này co giãn và có thể coi gần đúng như những lò xo có độ cứng tương đương là $k$. Các nghiên cứu y khoa cho thấy, nếu đầu người bị rung lắc với tần số 29 Hz thì thị lực sẽ mờ đi do tần số rung lắc này cộng hưởng với tần số dao động riêng của nhãn cầu. Nếu khối lượng trung bình của một nhãn cầu người bình thường là 7,5 g thì độ cứng tương đương của hệ thống cơ giữ nhãn cầu là bao nhiêu?
Hình 5. Nhãn cầu được giữ bởi các cơ trong hốc mắt
Hướng dẫn giải:
\(f=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\Rightarrow k=4\pi^2f^2m=4\pi^2.29^2.0,0075\approx249\) Hz

Bạn có thể đánh giá bài học này ở đây