Áp suất khí theo mô hình động học phân tử. Quan hệ giữa động năng phân tử và nhiệt độ SVIP

I. ÁP SUẤT CHẤT KHÍ THEO MÔ HÌNH ĐỘNG HỌC PHÂN TỬ

1. Tác dụng của một phân tử khí lên thành bình

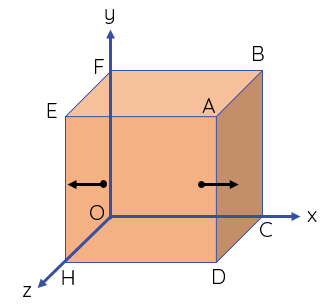
Xét một lượng khí gồm $N$ phân tử chứa trong một bình lập phương có cạnh $l$, trong hệ tọa độ vuông góc Oxyz.

Một phân tử khối lượng $m$ chuyển động thẳng đều song song với trục Ox với tốc độ \(\text{v}\) từ thành bình EFOH tới va chạm đàn hồi và trực diện với thành bình ABCD. Sau khi va chạm, phân tử chuyển động theo chiều ngược lại với tốc độ có cùng độ lớn \(\text{v}\) tới thành bình đối diện.

Do độ lớn của vận tốc tức thời và tốc độ tức thời của một chuyển động có độ lớn bằng nhau nên động lượng của phân tử trước khi va chạm với thành bình có giá trị là \(+m\text{v}\), sau khi va chạm với thành bình có giá trị là \(-m\text{v}\). Độ biến thiên động lượng của phân tử do va chạm với thành bình ABCD có độ lớn là:

\(\left|\Delta\overrightarrow{p}\right|=\left|-m\text{v}-\left(+m\text{v}\right)\right|=\left|-2m\text{v}\right|=2m\text{v}\)

Vận dụng các định luật cơ học Newton vào mô hình khí lí tưởng có thể xác định được áp suất của một phân tử khí tác dụng lên thành bình là \(p_m=\dfrac{m}{V}\text{v}^2\), với \(\text{v}\) là tốc độ chuyển động của phân tử, \(V\) là thể tích của lượng khí.

❗Chú ý về các kí hiệu:

- Động lượng kí hiệu là \(\overrightarrow{p}\).

- Áp suất của một lượng khí kí hiệu là \(p\).

- Áp suất của một phân tử khí kí hiệu là \(p_m\).

2. Tác dụng của N phân tử khí lên thành bình

Vì số phân tử $N$ vô cùng lớn và các phân tử chuyển động hỗn loạn trong bình nên các hướng Ox, Oy và Oz là bình đẳng. Do đó, số phân tử chuyển động theo hướng Ox, từ mặt EFOH sang mặt ABCD và ngược lại để gây áp suất lên hai mặt này chỉ bằng \(\dfrac{1}{3}\) số phân tử có trong bình \(\left(\dfrac{X}{3}\right)\).

Tốc độ của các phân tử không bằng nhau vì chúng chuyển động hỗn loạn, do đó áp suất của mỗi phân tử tác dụng lên thành bình cũng không bằng nhau. Trung bình mỗi phân tử tác dụng lên thành bình một áp suất \(\overline{p}_m=\dfrac{m}{V}\overline{\text{v}^2}\), trong đó:

\(\overline{\text{v}^2}=\dfrac{\text{v}_1^2+\text{v}_2^2+...+\text{v}_N^2}{N}\)

Đại lượng này được gọi là "trung bình của các bình phương tốc độ".

Từ đó, công thức tính áp suất của khí trong bình tác dụng lên thành bình ABCD là:

\(p=\dfrac{N}{3}\overline{p_m}=\dfrac{1}{3}\dfrac{Nm}{V}\overline{\text{v}^2}\)          (1)

Trong đó \(\dfrac{N}{V}\) là số phân tử có trong một đơn vị thể tích, gọi là mật độ phân tử. Nếu kí hiệu mật độ phân tử là \(\mu\), động năng trung bình của phân tử là \(W_đ=\dfrac{m\overline{\text{v}^2}}{2}\) và thay \(W_đ\) vào (1) ta được:

\(p=\dfrac{2}{3}\mu W_đ\)          (2)

Vì các mặt của hình lập phương là bình đẳng nên áp suất của chất khí tác dụng lên các mặt của bình đều như nhau và đều được xác định bằng các hệ thức (1), (2).

II. MỐI QUAN HỆ GIỮA ĐỘNG NĂNG PHÂN TỬ VÀ NHIỆT ĐỘ

Vì \(R\) và \(N_A\) đều là các hằng số có giá trị xác định, nên ta có thể tính được giá trị của hằng số \(k\):

\(k=\dfrac{R}{N_A}=1,38.10^{-23}\) J/K

Hằng số $k$ được gọi là hằng số Boltzmann.

Do đó, động năng trung bình của phân tử được xác định bằng hệ thức:

\(W_đ=\dfrac{3}{2}kT\)          (3)

Từ đó, có thể rút ra những hệ quả sau:

- Các khí có bản chất khác nhau, khối lượng khác nhau nhưng nhiệt độ như nhau thì động năng trung bình của các phân tử bằng nhau.

- Động năng trung bình của phân tử khí càng lớn thì nhiệt độ của khí càng cao.

- Vì \(\overline{W_đ}\) tỉ lệ thuận với $T$ nên người ta có thể coi nhiệt độ tuyệt đối là số đo động năng trung bình của phân tử theo một đơn vị khác.

1. Áp suất chất khí theo mô hình động học phân tử:

\(p=\dfrac{1}{3}\mu m\overline{\text{v}^2}=\dfrac{2}{3}\mu W_đ\)

Trong đó \(\mu\) là mật độ phân tử khí \(\left(\mu=\dfrac{N}{V}\right)\), \(\overline{\text{v}^2}\) là trung bình của các bình phương tốc độ phân tử.

2. Liên hệ giữa động năng trung bình của phân tử và nhiệt độ:

\(\overline{W_đ}=\dfrac{3}{2}kT\)

Trong đó $k$ là hằng số Boltzmann: \(k\) = 1,38.10^-23 J/K.