Áp suất - động năng của phân tử khí SVIP

1. ÁP SUẤT CỦA CHẤT KHÍ

➤ Ảnh hưởng của chuyển động các phân tử khí đến áp suất tác dụng lên thành bình

Khi các phân tử khí chuyển động nhiệt đến va chạm vào thành bình sẽ gây áp suất lên thành bình. Áp suất này được tính bằng áp lực của các phân tử khí tác dụng lên một đơn vị diện tích thành bình.

Áp suất khí tác dụng lên thành bình càng lớn khi các phân tử khí chuyển động nhiệt càng nhanh, khối lượng và mật độ phân tử khí càng lớn.

➤ Biểu thức áp suất khối khí tác dụng lên thành bình

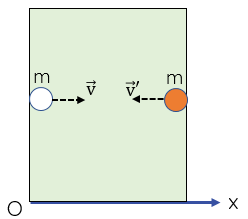
Một phân tử khí đập vuông góc với thành bình và bật ngược lại

Xét một phân tử khí có khối lượng $m$ chuyển động với vận tốc \(\overrightarrow{\text{v}}\) theo phương Ox đập vuông góc vào thành bình, Sau khi va chạm với thành bình, phân tử khí bật ngược lại với vận tốc \(\overrightarrow{\text{v}}'\). Khi đó lực do thành bình tác dụng lên phân tử trong thời gian va chạm \(\Delta t\) là:

\(\overrightarrow{f}=\dfrac{\Delta\overrightarrow{p}}{\Delta t}=\dfrac{m\left(\overrightarrow{\text{v}}'-\overrightarrow{\text{v}}\right)}{\Delta t}\)        (1)

Theo định luật III Newton, lực do phân tử khí tác dụng lên thành bình cũng có cùng độ lớn là \(f\). Chiếu (1) lên trục Ox ta được:

\(f=\left|\dfrac{m\left(-v'-v\right)}{\Delta t}\right|\)

Coi va chạm là hoàn toàn đàn hồi nên \(v'=v\).

Do đó \(f=\left|\dfrac{m\left(-v'-v\right)}{\Delta t}\right|=\dfrac{2mv}{\Delta t}\)

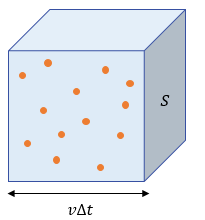
Minh họa các phân tử khí $N$ trong hình lập phương có cạnh là \(v\Delta t\), diện tích mặt bên là $S$

Xét khối khí trong một hình lập phương có cạnh là \(v\Delta t\), diện tích mặt bên là $S$. Gọi \(\mu\) là mật độ phân tử khí trong bình. Số phân tử khí trong hình lập phương là:

\(N=\mu Sv\Delta t\)

Sau thời gian \(\Delta t\), $N$ phân tử này đều có khả năng đến đập vào diện tích $S$ nếu vận tốc của chúng hướng về $S$. Vì các phân tử khí chuyển động nhiệt hỗn loạn, không có phương ưu tiên nên số lượng các phân tử khí đập vào mỗi mặt của hình lập phương là như nhau và bằng \(\dfrac{N}{6}\).

Tổng hợp lực do \(\dfrac{N}{6}\) phân tử khí tác dụng lên diện tích $S$ của thành bình là:

\(F=\dfrac{N}{6}.f=\dfrac{\mu Sv\Delta t}{6}.\dfrac{2mv}{\Delta t}=\dfrac{1}{3}\mu mv^2S\)

Áp suất tác dụng lên thành bình là:

\(p=\dfrac{F}{S}=\dfrac{1}{3}\mu mv^2\)         (2)

Trong công thức (2), \(v^2\) là trung bình của bình phương tốc độ chuyển động nhiệt của các phân tử \(\left(v^2=\dfrac{v_1^2+v_2^2+...+v_N^2}{N}\right)\). Khi đó:

\(p=\dfrac{1}{3}\mu m\overline{v^2}\)         (3)

Biểu thức áp suất chất khí tác dụng lên thành bình là:

\(p=\dfrac{1}{3}\mu m\overline{v^2}\)

Trong đó: \(\mu\) là mật độ phân tử khí; \(m,\) \(\overline{v^2}\) lần lượt là khối lượng và trung bình của bình phương tốc độ chuyển động nhiệt của các phân tử khí.

2. PHÂN TỬ KHÍ

Gọi \(W_đ\) là động năng trung bình của mỗi phân tử khí:

\(W_đ=\dfrac{1}{2}m\overline{v^2}\)

Thay vào (3) ta được: \(p=\dfrac{2}{3}\mu W_đ\)             (4)

Như vậy, áp suất khí tỉ lệ với động năng trung bình của mỗi phân tử.

Kết hợp với phương trình trạng thái khí lí tưởng và số Avogadro: \(N_A=\dfrac{\mu V}{n}=\dfrac{N}{n};\) \(pV=nRT.\)

Từ (4) rút ra được: \(W_đ=\dfrac{3}{2}\dfrac{R}{N_A}T\)

Đặt \(k=\dfrac{R}{N_A}=const\), khi đó: \(W_đ=\dfrac{3}{2}kT\)           (5)

Biểu thức (5) cho thấy động năng trung bình của mỗi phân tử khí tỉ lệ với nhiệt độ tuyệt đối của khí. Động năng này còn được gọi là động năng tịnh tiến trung bình của phân tử.

Hằng số \(k=\dfrac{R}{N_A}\) gọi là hằng số Boltzmann mang tên nhà vật lí người Áo Lugwig Eduard Boltzmann.

Hằng số Boltzmann $k$ là hằng số khí đặc trưng cho mối liên hệ giữa nhiệt độ và năng lượng. Giá trị của hằng số Boltzmann trong hệ SI bằng

\(k=\dfrac{R}{N_A}\approx1,38.10^{-23}\) J/K

Động năng tịnh tiến trung bình của phân tử khí tỉ lệ với nhiệt độ tuyệt đối của khí.

\(W_đ=\dfrac{3}{2}kT\)

 ❗Nội năng của khí lí tưởng

Giả sử $n$ mol khí lí tưởng mà chúng ta xét là loại đơn nguyên tử. Vì nội năng của khí lí tưởng bằng tổng động năng tịnh tiến trung bình của các phân tử khí.

Ta có: \(U=nN_AW_đ=nN_A\dfrac{3}{2}kT\)

Thay \(R=kN_A\) ta được:

\(U=\dfrac{3}{2}nRT\)

Nội năng của một khối lượng khí lí tưởng xác định chỉ phụ thuộc vào nhiệt độ.

1. Biểu thức áp suất chất khí tác dụng lên thành bình là:

\(p=\dfrac{1}{3}\mu m\overline{v^2}\)

2. Động năng tịnh tiến trung bình của phân tử khí tỉ lệ với nhiệt độ tuyệt đối của khí.

\(W_đ=\dfrac{3}{2}kT\)