Trước hết ta đi tìm phương trình đường thẳng MN.

Gọi phương trình đường thẳng MN là \(MN:y=ax+b\).

Do \(M\in MN\) nên \(2=-3a+b\) \(\Leftrightarrow b=3a+2\) (1)

Mặt khác \(N\in MN\) nên \(-2=3a+b\) (2)

Từ (1) và (2) \(\Rightarrow-2=3a+3a+2\) \(\Leftrightarrow6a=-4\) \(\Leftrightarrow a=-\dfrac{2}{3}\)

Từ đó \(\Rightarrow b=3.\left(-\dfrac{2}{3}\right)+2=0\) . Vậy đường thẳng MN chính là đường thẳng \(y=-\dfrac{2}{3}x\) đi qua gốc tọa độ O. Từ đây suy ra M, O, N thẳng hàng.

Ta thấy các hệ số \(a,b,c\) của phương trình đã cho thỏa mãn \(a-b+c=1-\left[-\left(m-3\right)\right]-m+2=1+m-3-m+2=0\)

nên phương trình đã cho sẽ có một nghiệm là \(-1\) và nghiệm kia là \(m-2\).

Trong hệ thức \(x_1^2+x_2=8\), vai trò của \(x_1,x_2\) không như nhau nên ta xét 2 trường hợp:

TH1: Nếu \(x_1=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(-1\right)^2+m-2=8\Leftrightarrow m=9\).

TH2: Nếu \(x_2=-1\) thì \(x_1^2+x_2=8\Leftrightarrow\left(m-2\right)^2-1=8\Leftrightarrow\left(m-2\right)^2=9\) \(\Leftrightarrow m-2=\pm3\) \(\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-1\end{matrix}\right.\). 

Vậy để phương trình đã cho có 2 nghiệm thỏa điều kiện đề cho thì \(\left[{}\begin{matrix}m=-1\\m=5\\m=9\end{matrix}\right.\)

a) Áp dụng định lý Thales trong tam giác ABC, ta có:

\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) . Kết hợp với giả thiết ta được \(\dfrac{2}{5}=\dfrac{AE}{7,5}\) \(\Rightarrow AE=3\)

b) Ta thấy \(\dfrac{AE}{AC}=\dfrac{3}{7,5}=\dfrac{2}{5}\) nhưng \(\dfrac{BF}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\ne\dfrac{AE}{AC}\) nên theo định lý Thales đảo, ta không thể có EF//AB.

 Nếu đề bài nói "Chỉ 2 bạn giỏi nhất mới được tham gia vòng tiếp theo" thì chỉ có 1 cách duy nhất vì 2 bạn học giỏi là một sự thật cố định. 

 Sửa lại đề một chút là "Chỉ có 2 bạn đạt thành tích cao nhất mới được tham gia vòng tiếp theo".

 Như vậy, việc "có 2 bạn đạt thành tích cao nhất" bao gồm 2 giai đoạn: Một bạn bất kì đạt thành tích tốt nhất và bạn tiếp theo đạt thành tích tốt thứ nhì. Ở giai đoạn thứ nhất, có 25 cách để sự kiện xảy ra (do có 25 bạn tham gia cuộc thi). Ở giai đoạn thứ hai, có 24 cách để sự kiện xảy ra (trừ 1 bạn ở giai đoạn thứ nhất). Do vậy, có tất cả \(25\times24=600\) (cách)

 Do \(A\left(2;-1\right)\) tiếp xúc với đường thẳng \(\Delta:-2x+10y-7=0\) nên \(d\left(A,\Delta\right)=R\) hay \(R=\dfrac{\left|-2.2+10.\left(-1\right)-7\right|}{\sqrt{\left(-2\right)^2+10^2}}=\dfrac{21\sqrt{26}}{52}\)

 Vậy bán kính của đường tròn cần tìm là \(R=\dfrac{21\sqrt{26}}{52}\)

Xét đường thẳng d₂, ta có: \(x=2+t\Rightarrow t=x-2\)

\(\Rightarrow y=6+2\left(x-2\right)=2x+2\) \(\Leftrightarrow2x-y+2=0\)

Vậy \(d_2:2x-y+2=0\)

Giao điểm của d₁ và d₂ thỏa mãn hệ phương trình:

\(\left\{{}\begin{matrix}4x+3my-m^2=0\\2x-y+2=0\end{matrix}\right.\). Để giao điểm này nằm trên trục tung thì \(x=0\). Do đó \(\left\{{}\begin{matrix}3my-m^2=0\\2-y=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=2\\6m-m^2=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)

Vậy để d₁ cắt d₂ tại 1 điểm trên trục tung thì \(m=0\) hoặc \(m=6\)

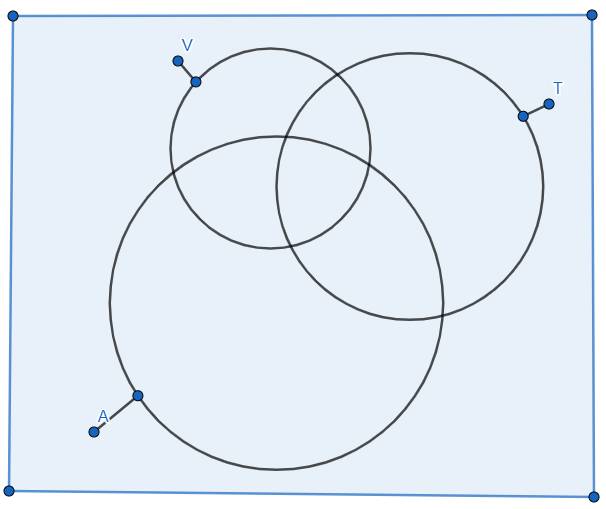
Gọi V, T, A lần lượt là tập hợp các học sinh giỏi Văn, Toán, Tiếng Anh. Theo đề bài, ta có: \(\left|V\right|=18;\left|T\right|=20;\left|A\right|=22\)\(;\left|V\cap T\cap A\right|=5\)\(;\left|A\cup T\cup V\right|=34\)

Áp dụng công thức bù trừ, ta có:

\(\left|V\cup T\cup A\right|=\left|V\right|+\left|T\right|+\left|A\right|-\left|V\cap T\right|-\left|T\cap A\right|-\left|A\cap V\right|+\left|V\cap T\cap A\right|\)

\(\Rightarrow34=18+20+22-P+5\) (với \(P=\left|V\cap T\right|+\left|T\cap A\right|+\left|A\cap V\right|\))

\(\Rightarrow P=31\)

Số học sinh thích đúng 1 môn trong 3 môn Toán, Văn, Tiếng Anh chính bằng:

\(\left|V\cup T\cup A\right|-P+2\left|V\cap T\cap A\right|\) \(=34-31+2.5=13\) (học sinh)

 Dễ dàng chứng minh rằng các số có dạng \(n^3\) khi chia cho 7 sẽ chỉ có các số dư là \(0,1,6\). (Bằng cách đặt \(n=7k+i\left(i=\overline{0,6}\right)\) rồi khai triển biểu thức \(\left(7k+i\right)^3=\left(7k\right)^3+3\left(7k\right)^2i+3.7k.i^2+i^3\) và xét số dư của \(i^3\) cho 7.

 Nếu trong 3 số a, b, c có 1 số chia hết cho 7 thì đương nhiên ta có đpcm.

 Nếu trong 3 số a, b, c không có số nào chia hết cho 7 (tức là không có số nào trong 3 số \(a^3,b^3,c^3\) chia hết cho 7), thì theo nguyên lí Dirichlet, tồn tại 2 số trong 3 số \(a^3,b^3,c^3\) có cùng số dư khi chia cho 7 (do lúc này chỉ còn 2 số dư là 1,6). Giả sử 2 số đó là \(a^3,b^3\). Khi đó \(a^3-b^3⋮7\) \(\Rightarrowđpcm\)

Vậy trong mọi trường hợp, ta đều có đpcm.