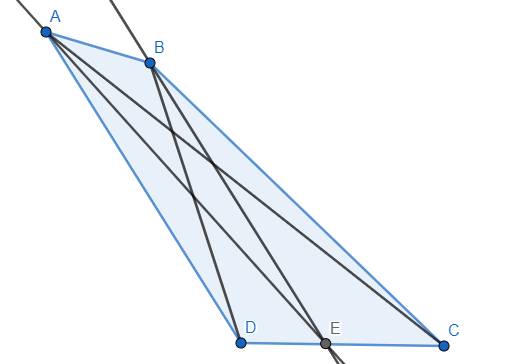
Áp dụng tính chất tia phân giác, ta có \(\dfrac{ED}{EC}=\dfrac{AD}{AC}\) và \(\dfrac{ED}{EC}=\dfrac{BD}{BC}\). Từ đó suy ra \(\dfrac{AD}{AC}=\dfrac{BD}{BC}\Rightarrow AD.BC=AC.BD\) (đpcm)

 Nếu bạn chưa thấy câu trả lời thì vào trang cá nhân của mình xem nhé.

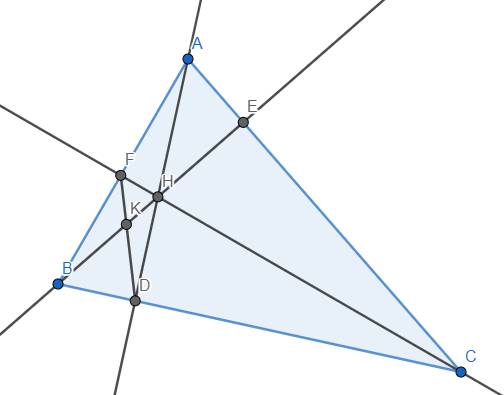
a) Dễ thấy \(\widehat{ADC}=\widehat{AFC}=90^o\) \(\Rightarrow\) Tứ giác ACDF nội tiếp đường tròn nhận AC làm đường kính \(\Rightarrow\) Tâm của đường tròn ngoại tiếp tứ giác ACDF chính là trung điểm của đoạn AC.

b) Áp dụng định lý Menelaus cho tam giác HBC với cát tuyến DFK, ta có \(\dfrac{KH}{KB}.\dfrac{DB}{DC}.\dfrac{FC}{FH}=1\) \(\Rightarrow\dfrac{KH}{KB}=\dfrac{DC}{DB}.\dfrac{FH}{FC}\) (1)

Áp dụng định lý Ceva cho tam giác HBC với các đường đồng quy CE, DH, BF và \(D\in BC,E\in HB,F\in HC\), ta có \(\dfrac{DC}{DB}.\dfrac{EB}{EH}.\dfrac{FH}{FC}=1\) \(\Rightarrow\dfrac{EH}{EB}=\dfrac{DC}{DB}.\dfrac{FH}{FC}\) (2)

Từ (1) và (2) suy ra \(\dfrac{KH}{KB}=\dfrac{EH}{EB}\) \(\Rightarrow\) đpcm

Để chọn ra 3 người có cả nam và nữ đi trực nhật thì có 2 phương án thực hiện: Chọn 1 nam, 2 nữ và chọn 1 nữ, 2 nam.

Xét phương án thứ nhất, có \(C^1_4=4\) cách chọn 1 bạn nam, \(C^2_3=3\) cách chọn 2 bạn nữ. Vậy có tất cả là \(4.3=12\) cách chọn.

Xét phương án thứ hai, có \(C^1_3=3\) cách chọn 1 bạn nữ và \(C^2_4=6\) cách chọn 2 bạn nam. Vậy có tất cả \(3.6=18\) cách chọn.

Như vậy, có tất cả là \(12+18=30\) cách chọn.

Mình bổ sung một cách làm khác nhé.

Áp dụng BĐT Cô-si cho 3 số dương \(a,b,c\), ta có \(a+b+c\ge3\sqrt[3]{abc}\) \(\Rightarrow1\ge3\sqrt[3]{abc}\)      (1)

Áp dụng BĐT Cô-si cho 3 số dương \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) ta có \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{\dfrac{1}{abc}}\)           (2)

Nhân theo vế của các BĐT (1) và (2), ta được \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge3\sqrt[3]{abc}.3\sqrt[3]{\dfrac{1}{abc}}=9\) (đpcm)

Đẳng thức xảy ra \(\Leftrightarrow a=b=c=\dfrac{1}{3}\)

a) \(\dfrac{x}{y}=\dfrac{1}{3}\Rightarrow y=3x\). Thay vào biểu thức N, ta có: \(N=\dfrac{x-3x}{x+9x}=\dfrac{-2x}{10x}=-\dfrac{1}{5}\)

b) \(x+y+1=0\Leftrightarrow x+y=-1\). Thay vào biểu thức M, ta có: \(M=\left(-1\right)^2-y^3\left(-1\right)+x^2-y^3+3\) \(=1+y^3+x^2-y^3+3\) \(=x^2+4\)

\(A=\dfrac{ab}{ab+a+1}+\dfrac{bc}{bc+b+1}+\dfrac{ca}{ca+c+1}\)

\(A=\dfrac{abc}{abc+ac+c}+\dfrac{bc}{bc+b+abc}+\dfrac{ca}{ca+c+1}\)

\(A=\dfrac{1}{1+ac+c}+\dfrac{c}{c+1+ac}+\dfrac{ca}{ca+c+1}\)

\(A=1\)