

Lê Song Phương
Giới thiệu về bản thân



































Do \(C\in d:x-2y+8=0\) nên \(C\left(2m-8;m\right)\)
Ta có \(AB=\sqrt{\left(5-2\right)^2+\left(1-2\right)^2}=\sqrt{10}\)
Phương trình đường thẳng AB có dạng:
\(AB:\dfrac{y-2}{x-2}=\dfrac{1-2}{5-2}=-\dfrac{1}{3}\) \(\Leftrightarrow3y-6=2-x\) \(\Leftrightarrow x+3y-8=0\)
Do đó \(d\left(C,AB\right)=\dfrac{\left|2m-8+3m-8\right|}{\sqrt{1^2+3^2}}=\dfrac{\left|5m-16\right|}{\sqrt{10}}\)
Mặt khác \(S_{ABC}=17\) \(\Leftrightarrow\dfrac{1}{2}AB.d\left(C,AB\right)=17\) \(\Leftrightarrow\dfrac{1}{2}.\sqrt{10}.\dfrac{\left|5m-16\right|}{\sqrt{10}}=17\) \(\Leftrightarrow\left|5m-16\right|=34\) (*)
Nếu \(m\ge\dfrac{16}{5}\) thì (*) \(\Rightarrow5m-16=34\Leftrightarrow m=10\) (nhận). Khi đó \(C\left(12;10\right)\)
Nếu \(m< \dfrac{16}{5}\) thì (*) \(\Rightarrow16-5m=34\) \(\Leftrightarrow m=-\dfrac{18}{5}\) (nhận). Khi đó \(C\left(-\dfrac{76}{5};-\dfrac{18}{5}\right)\)
Vậy có 2 điểm C thỏa nãm ycbt là \(C\left(12;10\right)\) và \(C\left(-\dfrac{76}{5};-\dfrac{18}{5}\right)\)
Ta có \(x^2+4x-5\ge0\) \(\Leftrightarrow\left(x-1\right)\left(x+5\right)\ge0\)
Đặt \(f\left(x\right)=\left(x-1\right)\left(x+5\right)\). Ta thấy \(1,-5\) là các nghiệm đơn của \(f\left(x\right)\). Ta lập bảng xét dấu:
| \(x\) | \(-\infty\) \(-5\) \(1\) \(+\infty\) |
| \(f\left(x\right)\) | \(+\) \(-\) \(0\) \(+\) |
Ta suy ra \(f\left(x\right)\ge0\Leftrightarrow\left[{}\begin{matrix}x\ge1\\x\le-5\end{matrix}\right.\)
Vậy bất phương trình đã cho có tập nghiệm \(S=\left\{x\inℝ|\left(x\ge1\right)V\left(x\le-5\right)\right\}\)
\(\Delta_fH^0_{298}=-542,83-2.167,16-\left(-795,0\right)\) \(=-82,15\left(kJ\right)\)
Một mặt, nếu hàm số \(f\left(x\right)\) có đồ thị hàm số không phải là đường thẳng (ví dụ như hàm số \(y=x^2\)) thì sẽ không tồn tại "phương trình đường thẳng của hàm số \(f\left(x\right)\)" nhưng vẫn sẽ tồn tại "đồ thi hàm số \(f\left(x\right)\)".
Mặt khác, cho dù \(f\left(x\right)\) có đồ thị là đường thẳng thì hai khái niệm này vẫn hoàn toàn khác nhau. "Phương trình đường thẳng của \(f\left(x\right)\)" là dùng để chỉ một phương trình đại số, còn "đồ thị hàm số \(f\left(x\right)\)" dùng để chỉ hình vẽ biểu thị hàm số đó.
Dễ thấy rằng \(\dfrac{DG}{DC}=\dfrac{1}{3}\) và \(\dfrac{BK}{BC}=\dfrac{3}{5}\)
Ta thấy \(\dfrac{DE}{EB}=\dfrac{DG}{AB}=\dfrac{DG}{CD}=\dfrac{1}{3}\) \(\Rightarrow\dfrac{DE}{BD}=\dfrac{1}{4}\) \(\Rightarrow DE=\dfrac{1}{4}BD=\dfrac{1}{4}.24=6\left(cm\right)\)
Mặt khác \(\dfrac{FB}{FD}=\dfrac{BK}{AD}=\dfrac{BK}{BC}=\dfrac{3}{5}\) \(\Rightarrow\dfrac{FB}{BD}=\dfrac{3}{8}\) \(\Rightarrow FB=\dfrac{3}{8}BD=\dfrac{3}{8}.24=9\left(cm\right)\)
\(\Rightarrow EF=BD-DE-FB=24-6-9=9\left(cm\right)\)
Vậy \(DE=6cm;EF=FB=9cm\)
đk: \(\left\{{}\begin{matrix}x\ge-1\\y\ge0\\x^2>y\end{matrix}\right.\)
pt đầu \(\Leftrightarrow\sqrt{\left(x+1\right)y}=2y-x-1\)
\(\Rightarrow\left(x+1\right)y=4y^2+x^2+1+2x-4xy-4y\)
\(\Leftrightarrow x^2+4y^2-5xy+2x-5y+1=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-4y\right)+\left(x-y\right)+\left(x-4y\right)+1=0\)
\(\Leftrightarrow\left(x-y+1\right)\left(x-4y+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=x+1\\x=4y-1\end{matrix}\right.\)
TH1: \(y=x+1\) thay vào pt thứ hai, ta được
\(\sqrt{2x+3}+\sqrt{x+1}=x^2-x-1\)
\(\Leftrightarrow\left(\sqrt{2x+3}-3\right)+\left(\sqrt{x+1}-2\right)=x^2-x-6\)
\(\Leftrightarrow\dfrac{2x-6}{\sqrt{2x+3}+3}+\dfrac{x-3}{\sqrt{x+1}+2}-\left(x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(\dfrac{2}{\sqrt{2x+3}+3}+\dfrac{1}{\sqrt{x+1}+2}-x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\\dfrac{2}{\sqrt{2x+3}+3}+\dfrac{1}{\sqrt{x+1}+2}-x+2=0\end{matrix}\right.\)
TH1.1: \(x=3\Rightarrow y=x+1=4\) (nhận)
TH1.2:\(\dfrac{2}{\sqrt{2x+3}+3}+\dfrac{1}{\sqrt{x+1}+2}-x+2=0\) (chỗ này mai mình nghĩ tiếp)
TH2: \(x=4y-1\). Thay vào pt thứ hai, ta được
\(\sqrt{8y+1}+\sqrt{y}=16y^2-9y+1\)
\(\Leftrightarrow\left(\sqrt{8y+1}-1\right)+\sqrt{y}=16y^2-9y\)
\(\Leftrightarrow\dfrac{8y}{\sqrt{8y+1}+1}+\dfrac{y}{\sqrt{y}}-16y^2+9y=0\)
\(\Leftrightarrow y\left(\dfrac{8}{\sqrt{8y+1}+1}+\dfrac{1}{\sqrt{y}}-16y+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=0\\\dfrac{8}{\sqrt{8y+1}+1}+\dfrac{1}{\sqrt{y}}-16y+9=0\end{matrix}\right.\)
TH2.1: \(y=0\) \(\Rightarrow x=4y-1=-1\) (nhận)
TH2.2: \(\dfrac{8}{\sqrt{8y+1}+1}+\dfrac{1}{\sqrt{y}}-16y+9=0\)
(đoạn này để mai mình nghĩ tiếp nhé, ta tìm được các nghiệm \(\left(x;y\right)=\left(-1;0\right);\left(3;4\right)\))
a) Tọa độ vector pháp tuyến của đường BC là \(\overrightarrow{n_{BC}}=\left(1;-1\right)\)
\(\Rightarrow\) Tọa độ vector pháp tuyến của đường AH là \(\overrightarrow{n_{AH}}=\left(1;1\right)\)
\(\Rightarrow AH:x+y+m=0\) với \(m\inℝ\)
Mà AH đi qua A nên tọa độ điểm A thỏa mãn pt đường thẳng AH \(\Rightarrow-1-2+m=0\) \(\Leftrightarrow m=3\)
Vậy \(AH:x+y+3=0\)
b) Gọi d là đường thẳng chứa đường trung bình ứng với cạnh BC của tam giác ABC. Khi đó \(d//BC\) nên \(\overrightarrow{n_{BC}}=\overrightarrow{n_d}=\left(1;-1\right)\) (với \(\overrightarrow{n_d}\) là vector pháp tuyến của đường thẳng d) \(\Rightarrow d:x-y+n=0\) \(\left(n\inℝ\right)\)
Mặt khác, tọa độ H là nghiệm của hệ \(\left\{{}\begin{matrix}x-y+4=0\\x+y+3=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{7}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow H\left(-\dfrac{7}{2};\dfrac{1}{2}\right)\)
Gọi \(I\left(x_I;y_I\right)\) là trung điểm AH \(\Rightarrow\) \(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_H}{2}=\dfrac{-1-\dfrac{7}{2}}{2}=-\dfrac{9}{4}\\y_I=\dfrac{y_A+y_H}{2}=\dfrac{-2+\dfrac{1}{2}}{2}=-\dfrac{3}{4}\end{matrix}\right.\)
Do d là đường trung bình ứng với cạnh BC của tam giác ABC nên d đi qua trung điểm I của đường cao AH \(\Rightarrow-\dfrac{9}{4}-\left(-\dfrac{3}{4}\right)+n=0\) \(\Leftrightarrow n=\dfrac{3}{2}\) \(\Rightarrow d:x-y+\dfrac{3}{2}=0\)
Theo đề bài, giá bán \(x\) sản phẩm là \(170x\) (nghìn đồng)
Để nhà sản xuất không bị lỗ thì \(P\left(x\right)\le170x\) \(\Leftrightarrow x^2+30x+3300\le170x\) \(\Leftrightarrow x^2-140x+3300\le0\) \(\Leftrightarrow\left(x-110\right)\left(x-30\right)\le0\)
Đặt \(f\left(x\right)=\left(x-110\right)\left(x-30\right)\). Ta lập bảng xét dấu:
| \(x\) | \(-\infty\) \(30\) \(110\) \(+\infty\) |
| \(f\left(x\right)\) | \(+\) \(0\) \(-\) \(0\) \(+\) |
Vậy \(f\left(x\right)\le0\Leftrightarrow x\in\left[30;110\right]\). Do đó, để nhà sản xuất không bị lỗ thì số sản phẩm được sản xuất trong đoạn \(\left[30;110\right]\).
Sửa lại đề một chút là \(E=125\left(1+6+6^2+6^3+...+6^{2021}\right)\) nhé.
Xét biểu thức \(P=1+6+6^2+6^3+...+6^{2021}\)
\(\Rightarrow6P=6+6^2+6^3+6^4+...+6^{2022}\)
\(\Rightarrow5P=6P-P=6^{2022}-1\) \(\Rightarrow P=\dfrac{6^{2022}-1}{5}\)
Vậy \(E=125P=25\left(6^{2022}-1\right)\) \(=25.6^{2022}-25\)
\(\Rightarrow E+25=25.6^{2022}=\left(5.6^{1011}\right)^2\) là số chính phương.
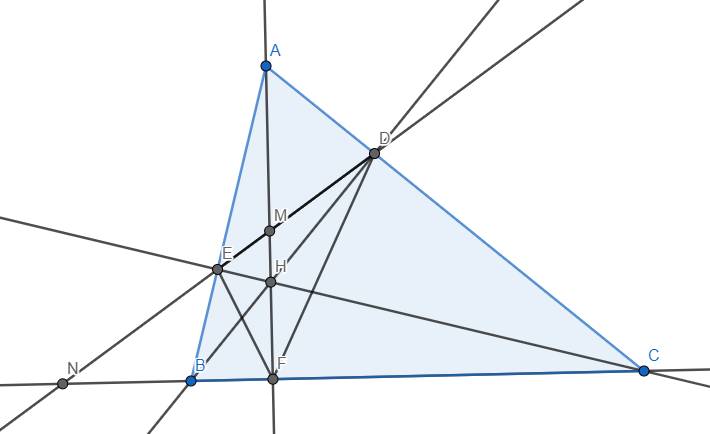
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)