

Lê Song Phương
Giới thiệu về bản thân



































Ta có \(A=\dfrac{1.5.6\left(1+2+4+9\right)}{1.3.5\left(1+2+4+9\right)}\)
\(A=\dfrac{1.5.6}{1.3.5}\)
\(A=2\)
pt đã cho \(\Leftrightarrow\left(x-y\right)\left(x+3y\right)=2x+6y-x+y\)
\(\Leftrightarrow\left(x-y\right)\left(x+3y\right)=2\left(x+3y\right)-\left(x-y\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a\\x+3y=b\end{matrix}\right.\) với \(a,b\inℤ\) và \(b\ge4\)
pt thành \(ab=2a-b\)
\(\Leftrightarrow ab-2a+b-2=-2\)
\(\Leftrightarrow\left(a+1\right)\left(b-2\right)=-2\) (*)
Vì \(b\ge4\Leftrightarrow b-2\ge2\). Do đó (*) \(\Rightarrow\) \(b-2=2\) hay \(b=4\), nghĩa là dấu "=" phải xảy ra \(\Leftrightarrow x=y=1\). Thử lại, ta thấy không thỏa mãn.
Vậy pt đã cho không có nghiệm nguyên dương.
Điểm F ở câu a) với điểm N ở câu b) là những điểm gì thế bạn? Mình thấy trong đề không có định nghĩa các điểm này.
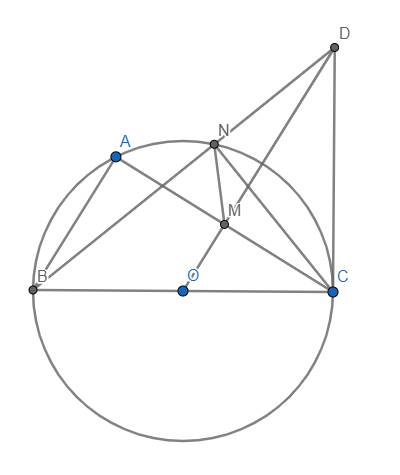
a) Xét đường tròn (O) có OM vuông góc với dây cung AC tại M
\(\Rightarrow\) M là trung điểm AC
\(\Rightarrow MA=MC=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Tam giác OCM vuông tại M nên \(OM=\sqrt{OC^2-MC^2}\) \(=\sqrt{5^2-3^2}\) \(=4\left(cm\right)\)
b) Vì DC là tiếp tuyến tại C của (O) nên \(CD\perp OC\) hay \(\Delta OCD\) vuông tại C
Xét \(\Delta OCD\) vuông tại C có đường cao CM nên \(DC^2=DM.DO\) (hệ thức lượng trong tam giác vuông)
c) Xét đường tròn (O) có đường kính BC nên \(\widehat{BNC}=90^o\) hay \(CN\perp BD\) tại N.
Xét tam giác BCD vuông tại C có đường cao CN nên \(DC^2=DN.DB\)
Từ đó suy ra \(DM.DO=DN.DB\left(=DC^2\right)\) \(\Rightarrow\dfrac{DM}{DB}=\dfrac{DN}{DO}\)
Xét \(\Delta DMN\) và \(\Delta DBO\), có:
\(\widehat{BDO}\) chung, \(\dfrac{DM}{DB}=\dfrac{DN}{DO}\)
\(\Rightarrow\Delta DMN~\Delta DBO\left(c.g.c\right)\)
\(\Rightarrow\widehat{DMN}=\widehat{NBO}\)
Lại có \(\widehat{DMN}+\widehat{NMO}=180^o\)
\(\Rightarrow\) đpcm
Giả sử có hữu hạn số nguyên tố là \(p_1,p_2,...,p_n\) với \(n\ge1\)
Gọi \(p_i\left(1\le i\le n\right)\) là số nguyên tố lớn nhất trong n số nguyên tố trên. Xét số \(P=p_1p_2...p_n+1\), rõ ràng \(P>p_i\) . Hơn nữa \(P\) không chia chết cho bất kì số nguyên tố \(p_j\left(1\le j\le n\right)\) nào nên \(P\) cũng là một số nguyên tố.
Như vậy, ta tìm được một số nguyên tố mới lớn hơn \(p_i\) là số nguyên tố lớn nhất. Điều này là vô lí.
Vậy điều giả sử là sai \(\Rightarrow\) Có vô hạn số nguyên tố.
Ta có \(\dfrac{a+b}{c}=\dfrac{b+c}{a}=\dfrac{a+c}{b}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, thu được:
\(\dfrac{a+b}{c}=\dfrac{b+c}{a}=\dfrac{a+c}{b}=\dfrac{a+b+b+c+a+c}{c+a+b}\) \(=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\b+c=2a\\c+a=2b\end{matrix}\right.\)
Trừ theo vế 2 hệ thức đầu tiên, ta có
\(\left(a+b\right)-\left(b+c\right)=2c-2a\)
\(\Leftrightarrow a-c=2\left(c-a\right)\)
\(\Leftrightarrow3\left(c-a\right)=0\)
\(\Leftrightarrow c=a\)
Hoàn toàn tương tự, ta có \(a=b=c\)
Do đó \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=1\)
Vậy \(P=\left(1+\dfrac{a}{b}\right)\left(1+\dfrac{b}{c}\right)\left(1+\dfrac{c}{a}\right)\)
\(=\left(1+1\right)\left(1+1\right)\left(1+1\right)\)
\(=8\)
a) Có \(\dfrac{2x-y}{x+y}=\dfrac{2}{7}\)
\(\Leftrightarrow7\left(2x-y\right)=2\left(x+y\right)\)
\(\Leftrightarrow14x-7y=2x+2y\)
\(\Leftrightarrow12x=9y\)
\(\Leftrightarrow\dfrac{x}{y}=\dfrac{9}{12}=\dfrac{3}{4}\)
b) Ta có \(\dfrac{t}{y}=\dfrac{4}{9}\) và \(\dfrac{z}{t}=\dfrac{5}{8}\)
\(\Rightarrow\dfrac{t}{y}.\dfrac{z}{t}=\dfrac{4}{9}.\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{z}{y}=\dfrac{5}{18}\)
\(\Leftrightarrow\dfrac{y}{z}=\dfrac{18}{5}\)
Lại có \(\dfrac{x}{y}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{x}{y}.\dfrac{y}{z}=\dfrac{2}{3}.\dfrac{18}{5}\)
\(\Leftrightarrow\dfrac{x}{z}=\dfrac{12}{5}\)

Trong tam giác ABC có \(\widehat{B}< \widehat{C}\) nên \(AC< AB\) (quan hệ giữa góc và cạnh đối diện trong tam giác)
Hơn nữa, vì AH là đường cao của tam giác ABC nên BH, CH lần lượt là hình chiếu của AB, AC trên đường thẳng BC.
\(\Rightarrow CH< BH\) (quan hệ đường xiên - hình chiếu)
(Bạn xem lại đề bài nhé, mình nghĩ nó là \(BH>HC\) đó. Nhìn từ hình vẽ cũng có thể thấy. Ý thứ 2 cũng vậy, mình nghĩ là \(BD>DC\))
TH \(p=3k+2\) thì suy ra \(k\) lẻ \(\Rightarrow k=2n+1\) rồi xét tương tự nhé
Vì \(p\) là số nguyên tố lớn hơn 3 nên \(p\) có dạng \(3k+1\) hoặc \(3k+2\)
TH1: Nếu \(p=3k+1\) thì vì p là SNT nên \(k\) chẵn \(\Rightarrow k=2n\) \(\Rightarrow p=6n+1\)
\(\Rightarrow\)\(P=\left(p-1\right)\left(p+1\right)\)
\(=6n\left(6n+2\right)\)
\(=12n\left(3n+1\right)\)
Nếu \(n\) chẵn thì \(n\left(3n+1\right)⋮2\) \(\Rightarrow P=12n\left(3n+1\right)⋮12.2=24\)
Nếu \(n\) lẻ thì \(3n+1⋮2\) \(\Rightarrow P=12n\left(3n+1\right)⋮12.2=24\)
Vậy \(P⋮24\), đpcm.