Nguyễn Chí Thức
Giới thiệu về bản thân



































I live in vinh yen
47
I love it
I don't like chatting online
I use computer
1. I went to Laos.
2.I visited my grandparents.
3.yes , she does.
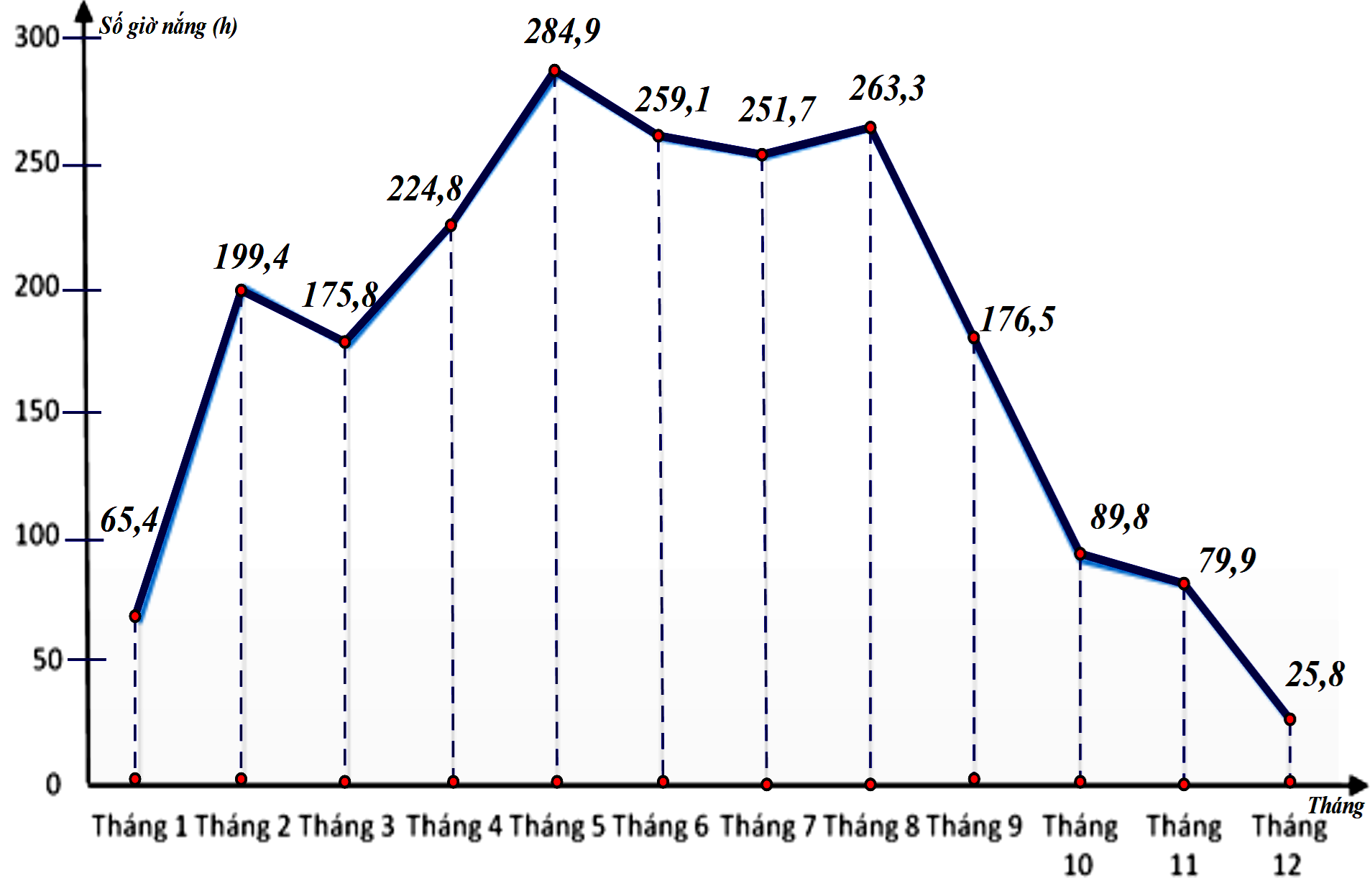
Biểu đồ cột kép là biểu đồ thích hợp biểu diễn bảng số liệu trên.
| GT | Hình thoi có , Vẽ vuông góc với cạnh , trên tia đối của lấy điểm sao cho . Nếu với , với . |
| KL | a) Chứng minh rằng là hình thoi. b) Ba điểm thẳng hàng. c) . |

a) Vì là hình thoi nên .
Xét tam giác , ta có , do đó tam giác là tam giác cân. Mặt khác . Từ đó suy tam giác là tam giác đều.
Trong tam giác đều, có đường cao , vậy BH cũng là đường trung tuyến của tam giác , hay H là trung điểm của .
Tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường, suy ra là hình bình hành.
Mặt khác, ta có nên ta suy ra là hình thoi.
b) Vì là hình thoi nên .
Vì là hình thoi nên .
Từ hai điều trên, theo tiên đề Euclid, ta suy ra
c)

Vì tam giác đều nên .
là hình thoi nên .
là hình thoi nên .
Xét tứ giác có:
+)
+) .
Suy ra tứ giác là hình thang cân. Do đó, (hai đường chéo bằng nhau).
| GT | Hình thoi có , Vẽ vuông góc với cạnh , trên tia đối của lấy điểm sao cho . Nếu với , với . |
| KL | a) Chứng minh rằng là hình thoi. b) Ba điểm thẳng hàng. c) . |

a) Vì là hình thoi nên .
Xét tam giác , ta có , do đó tam giác là tam giác cân. Mặt khác . Từ đó suy tam giác là tam giác đều.
Trong tam giác đều, có đường cao , vậy BH cũng là đường trung tuyến của tam giác , hay H là trung điểm của .
Tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường, suy ra là hình bình hành.
Mặt khác, ta có nên ta suy ra là hình thoi.
b) Vì là hình thoi nên .
Vì là hình thoi nên .
Từ hai điều trên, theo tiên đề Euclid, ta suy ra
c)

Vì tam giác đều nên .
là hình thoi nên .
là hình thoi nên .
Xét tứ giác có:
+)
+) .
Suy ra tứ giác là hình thang cân. Do đó, (hai đường chéo bằng nhau).
a)
b) .
hoặc .
a) x3 + 8y3 = x3 + (2y)3 = ( x + 2y ).(x2 - 2xy + 4y2 )
B) x2 + 2xy + y2 - 4 = ( x + y )2 - 22 = ( x + y - 2).(x + y + 2 )
a) ;
b) .
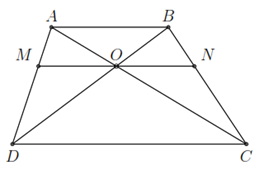
Xét có // nên theo định lí Thalès ta có
. (1)
Xét có // nên theo định lí Thalès ta có
. (2)
Xét có // nên theo định lí Thalès ta có
. (3)
Từ , , suy ra .
Suy ra .