Ta có hình vẽ:

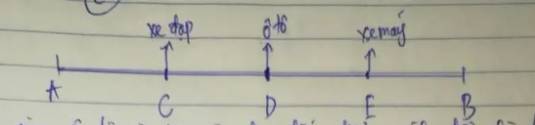
Gọi thời gian oto; xe máy và xe đạp đi đến điểm cách đầu là n (giờ)

Oto cách đều xe đạp và xe máy nên khoảng cách từ oto đến xe đạp bằng khoảng cách từ xe oto đến xe máy

Như vậy, đoạn thẳng CD bằng đoạn thẳng DE.( CD = DE )

Quãng đường oto đi là:

AD = 55xn

Quãng đường xe đạp đi là:

AC = 15xn

Xe máy đi sau 36 phút ( Đổi 36 phút = 0,6 giờ ) nên thời gian xe máy đi là:

n = 0,6 ( giờ )

Quãng đường xe máy đi là:

BE = 50x( t - 0,6 )

Mà CD = DE

Như vậy AD - AC  = AB - AD - BE

Nên: 2AD = AB - BE + AC

Nên: 2x55xn = 202 - 50x( n- 0,6 ) + 15xn

Nên: 145xn = 202 + 50x0,6 = 232

 n = 232/145 = 1,6 ( giờ )

thể tích khối lập phương là: 9x9x9x7 = 51039(cm³)

                                                            Đáp số: 5103 cm³

 Gỉa sử số nguyên dương `n` có `a` chữ số 
Ta có : 
 `\overline{2014n} \vdots 101`
`=>2014.10^a+n`
`=>[(19.100+95).10^a+n] \vdots 101`
`=>(19.101.10^a+95.10^a+n) \vdots 101`
`=>995.10^a+n) \vdots 101`
Vì `n` có giá trị nhỏ nhất nhất `a` cũng có giá trị nhỏ nhất
 + Nếu `a=1` thì :
`(950+n) \vdots 101`
`=>(9.101+41+n) \vdots 101`
`=>(41+n) \vdots 101` ( loại , vì `41+n<101` )
 + Nếu `a=2` thì :
`(9500+n) \vdots 101`
`=>(94.101+6+n) \vdots 101`
`=>(6+n) \vdots 101` ( nhận )
Vì số nguyên dương `n` nhỏ nhất và có `2` chữ số nên `n=95` `->đpcm`
Vậy : Số nguyên dương `n` là `95`