\(x^8-x^7+x^2-x+1>0\)

<=> \(x\left(x-1\right)\left(x^6+1\right)+1>0\)

<=> \(x\left(x-1\right)\left(x^6+1\right)>-1\)

<=>\(\left[{}\begin{matrix}x>-1\\x-1>-1\\x^6+1>-1\end{matrix}\right.\)

<=> \(\left[{}\begin{matrix}x>-1\\x>0\\x^6>-2\end{matrix}\right.\)

<=> \(\left[{}\begin{matrix}x>-1\\x>0\\x\in R\end{matrix}\right.\)

Xét từng trường hợp:

x > -1 (loại). Vì không thỏa mãn điều kiện.

x > 0 (loại). Vì không thỏa mãn điều kiện.

x ϵ R (nhận). Vì thỏa mãn điều kiện (đpcm)

A community helper I admire is a doctor. Physicians and surgeons diagnose and treat injuries or illnesses and address health maintenance. Physicians examine patients; take medical histories; prescribe medications; and order, perform, and interpret diagnostic tests. They often counsel patients on diet, hygiene, and preventive healthcare. I feel grateful for doctors because they help us grow and healthy every day.

a/ \(\dfrac{8\sqrt{2}-\sqrt{32}-4}{1-\sqrt{2}}\)

 = \(\dfrac{-4\left(2\sqrt{2}-\sqrt{2}-1\right)}{1-\sqrt{2}}\)

 = \(\dfrac{-4\left(1-\sqrt{2}\right)}{1-\sqrt{2}}\)

 = -4

b/ ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x-4\ne0\\\sqrt{x}+2\ne0\\\sqrt{x}-2\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)

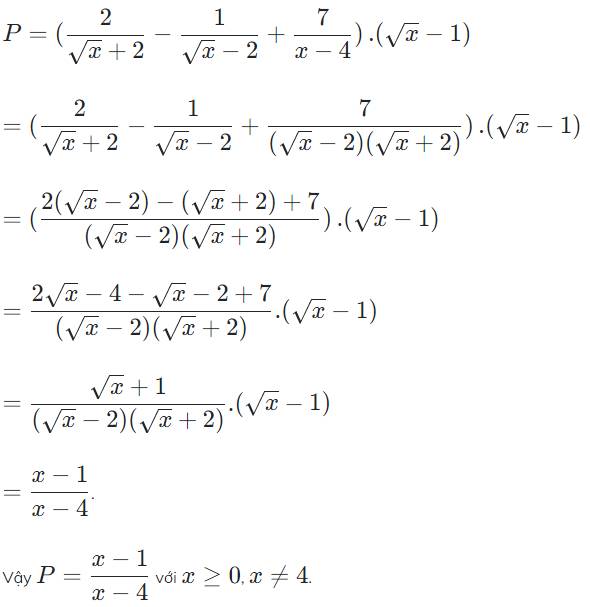
Đổi: 20 phút = \(\dfrac{1}{3}giờ\)

Gọi s (km) là quãng đường từ thành phố về quê (s > 0).

Thời gian từ thành phố về quê là: \(\dfrac{s}{30}+\dfrac{1}{3}\) (giờ)

Thời gian từ quê lên thành phố là: \(\dfrac{s}{25}\) (giờ)

Ta có phương trình:

 \(\dfrac{s}{25}\)= \(\dfrac{s}{30}+\dfrac{1}{3}\)

\(\dfrac{6s}{25.6}\)=\(\dfrac{5s}{30.5}+\dfrac{50}{3.50}\)

6s = 5s + 50

6s - 5s = 50

s = 50 (nhận)

Vậy quãng đường từ thành phố về quê là 50 km.

a/ 3x - 5 = 4          b/ \(\dfrac{2x}{3}+\dfrac{3x-1}{6}=\dfrac{x}{2}\)

    3x = 4 + 5             \(\dfrac{2x.2}{3.2}+\dfrac{3x-1}{6}=\dfrac{x.3}{2.3}\)

    3x = 9       

      x = \(\dfrac{9}{3}=3\)            4x + 3x - 1 = 3x

Vậy: S = {3}              7x - 1 = 3x

                                 7x - 3x = 1

                                  4x = 1

                                    x = \(\dfrac{1}{4}\)

                                Vậy: S = {\(\dfrac{1}{4}\)}

a/ 3x - 4 = 5 + x

    3x - x = 5 + 4

    2x = 9

      x = \(\dfrac{9}{2}\)

Vậy: S = {\(\dfrac{9}{2}\)}

b/ 3(x - 1) - 7 = 5(x + 2)

    3x - 3 - 7 = 5x + 10

    3x - 10 = 5x + 10

    (-10) - 10 = 5x - 3x

    -20 = 2x

     x = \(\dfrac{-20}{2}\)

     x = -10

Vậy: S = {-10}