olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Ôn tập và kiểm tra chương Hàm số và phương trình lượng giác SVIP

Tải ma trận In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):
Câu 2 (1đ):

Đổi số đo góc 105∘105^\circ sang rađian ta được

7π12\dfrac{7\pi }{12}.
5π12\dfrac{5\pi }{12}.
5π8\dfrac{5\pi }{8}.
9π12\dfrac{9\pi }{12}.
Câu 3 (1đ):

Cho hai góc nhọn aa và bb với tan⁡a=17\tan a=\dfrac{1}{7} và tan⁡b=34\tan b=\dfrac{3}{4}. Tổng a+ba+b bằng

π6.\dfrac{\pi }{6}.
π4.\dfrac{\pi }{4}.
π3.\dfrac{\pi }{3}.
2π3.\dfrac{2\pi }{3}.
Câu 4 (1đ):

Hàm số nào sau đây là hàm số tuần hoàn với chu kì bằng 2π2\pi ?

y=sin⁡xy=\sin x.
y=sin⁡2xy=\sin 2x.
y=tan⁡xy=\tan x.
y=cot⁡xy=\cot x.
Câu 5 (1đ):

Tập xác định của hàm số y=f(x)=cot⁡xy=f\left(x \right)=\cot x là

R\{kπ ∣ k∈Z}\mathbb{R}\backslash \left\{ k\pi \, \big| \, k\in \mathbb{Z} \right\}.
R\{π2+kπ ∣ k∈Z}\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi \, \big| \, k\in \mathbb{Z} \right\}.
R\{π2+k2π ∣ k∈Z}\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k2\pi \, \big| \, k\in \mathbb{Z} \right\}.
R\{2kπ ∣ k∈Z}\mathbb{R}\backslash \left\{ 2k\pi \, \big| \, k\in \mathbb{Z} \right\}.
Câu 6 (1đ):

Nghiệm của phương trình sin⁡x2=1\sin \dfrac{x}{2}=1 là

x=k2π, (k∈Z)x=k2\pi, \, \left(k\in \mathbb{Z} \right).
x=π+k2π, (k∈Z)x=\pi +k2\pi, \, \left(k\in \mathbb{Z} \right).
x=π+k4π, (k∈Z)x=\pi +k4\pi, \, \left(k\in \mathbb{Z} \right).
x=k4π, (k∈Z)x=k4\pi, \, \left(k\in \mathbb{Z} \right).
Câu 7 (1đ):

Tập nghiệm của phương trình tan⁡x=3\tan x=\sqrt{3} là

{π6+kπ ∣ k∈Z}\Big\{ \dfrac{\pi }{6}+k\pi \, \Big| \,k\in \mathbb{Z} \Big\}.
{π3+kπ ∣ k∈Z}\Big\{ \dfrac{\pi }{3}+k\pi \, \Big| \, k\in \mathbb{Z} \Big\}.
{π3+k2π ∣ k∈Z}\Big\{ \dfrac{\pi }{3}+k2\pi \, \Big| \,k\in \mathbb{Z} \Big\}.
{π6+k2π ∣ k∈Z}\Big\{ \dfrac{\pi }{6}+k2\pi \, \Big| \,k\in \mathbb{Z} \Big\}.
Câu 8 (1đ):

Cho tan⁡α=12\tan \alpha =12 với α∈(π;3π2)\alpha \in \Big(\pi ;\dfrac{3\pi }2\Big). Giá trị của sin⁡α\sin \alpha là

−12145-\dfrac{12}{\sqrt{145}}.
1145\dfrac{1}{\sqrt{145}}.
−1145-\dfrac{1}{\sqrt{145}}.
12145\dfrac{12}{\sqrt{145}}.
Câu 9 (1đ):

Hàm số nào sau đây là hàm số lẻ?

y=x2sin⁡(x+3)y=x^2\sin (x+3).
y=2x+cos⁡xy=2x+\cos x.
y=cos⁡3xy=\cos 3x.
y=cos⁡xx3y=\dfrac{\cos x}{x^3}.
Câu 10 (1đ):

Tập xác định của hàm số y=tan⁡(2x−π3)y=\tan \Big(2x-\dfrac{\pi }{3} \Big) là

D=R\{x≠π2+kπ ∣ k∈Z}D=\mathbb{R}\backslash \Big\{ x\ne \dfrac{\pi }{2}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
D=R\{x≠5π12+kπ2 ∣ k∈Z}D=\mathbb{R}\backslash \Big\{ x\ne \dfrac{5\pi }{12}+\dfrac{k\pi }{2} \, \big| \, k\in \mathbb{Z} \Big\}.
D=R\{x≠5π12+kπ ∣ k∈Z}D=\mathbb{R}\backslash \Big\{ x\ne \dfrac{5\pi }{12}+k\pi \, \big| \, k\in \mathbb{Z} \Big\}.
D=R\{x≠π6+kπ2 ∣ k∈Z}D=\mathbb{R}\backslash \Big\{ x\ne \dfrac{\pi }{6}+\dfrac{k\pi }{2} \, \big| \, k\in \mathbb{Z} \Big\}.
Câu 11 (1đ):

Số nghiệm phương trình sin⁡3xcos⁡x+1=0\dfrac{\sin 3x}{\cos x+1}=0 thuộc đoạn [2π;4π]\left[ 2\pi ;4\pi \right] là

44.
66.
55.
77.
Câu 12 (1đ):

Tổng tất cả các nghiệm của phương trình cot⁡x=3\cot x=\sqrt{3} trên đoạn [0 ; 2π]\left[ 0\ ;\ 2\pi \right] bằng

π6\dfrac{\pi }{6}.
5π6\dfrac{5\pi }{6}.
7π6\dfrac{7\pi }{6}.
4π3\dfrac{4\pi }{3}.
Câu 13 (1đ):

Cho góc α, (0∘<α<180∘)\alpha, \, \left(0^\circ <\alpha <180^\circ \right) thỏa mãn tan⁡α=3\tan \alpha =3.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) cot⁡α=13\cot \alpha =\dfrac{1}{\sqrt{3}}.
b) cos⁡α>0\cos \alpha >0.
c) sin⁡α=31010\sin \alpha =\dfrac{3\sqrt{10}}{10}.
d) 2sin⁡α−3cos⁡α3sin⁡α+2cos⁡α=−311\dfrac{2\sin\alpha -3\cos\alpha }{3\sin\alpha +2\cos\alpha }=\dfrac{-3}{11}.
Câu 14 (1đ):

Cho hàm số f(x)=∣x∣sin⁡xf(x)=|x|\sin x.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Tập xác định của hàm số là D=R\{0}D=\mathbb{R}\backslash \left\{ 0 \right\}.
b) f(−π)+f(π)=0f(-\pi)+f(\pi) = 0.
c) f(−x)=−f(x)f(-x)=-f(x).
d) Hàm số đã cho đối xứng qua gốc tọa độ O(0;0)O\left(0;0 \right).
Câu 15 (1đ):

Cho hai đồ thị hàm số y=sin⁡(x+π4)y=\sin \Big(x+\dfrac{\pi }{4}\Big) và y=sin⁡xy=\sin x.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: sin⁡(x+π4)=sin⁡x\sin \Big(x+\dfrac{\pi }{4}\Big)=\sin x.
b) Hoành độ giao điểm của hai đồ thị là x=3π8+kπ, ( k∈Z)x=\dfrac{3\pi }{8}+k\pi, \,(\, k\in \mathbb{Z}).
c) Khi x∈ [0;2π]x \in \,[0;2\pi ] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi x∈ [0;2π]x\in \,[0;2\pi ] thì toạ độ giao điểm của hai đồ thị hàm số là: (5π8;sin⁡5π8)\Big(\dfrac{5\pi }{8};\sin \dfrac{5\pi }{8} \Big); (7π8;sin⁡7π8)\Big(\dfrac{7\pi }{8};\sin \dfrac{7\pi }{8} \Big).
Câu 16 (1đ):

Một vật dao động xung quanh vị trí cân bằng theo phương trình x=1,5cos⁡(tπ4)x=1,5\cos \Big(\dfrac{t\pi }{4}\Big); trong đó tt là thời gian được tính bằng giây và quãng đường h=∣x∣h=|x| được tính bằng mét là khoảng cách theo phương ngang của vật đối với vị trí cân bằng.

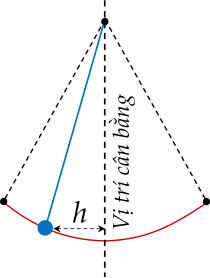
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Vật ở xa vị trí cân bằng nhất nghĩa là h=1,5h=1,5 m.
b) Trong 1010 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì cos⁡(tπ4)=0\cos \Big( \dfrac{t\pi }{4} \Big)=0.
d) Trong khoảng từ 00 đến 2020 giây thì vật đi qua vị trí cân bằng 44 lần.
Câu 17 (1đ):

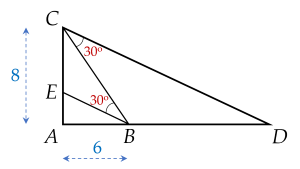
loading...

Cho tam giác ABCABC vuông tại AA có cạnh AB=6, AC=8AB=6, \, AC=8. Điểm EE thuộc đoạn ACAC sao cho CBE^=30∘\widehat{CBE}=30^\circ, điểm DD thuộc tia đối của tia BABA sao cho BCD^=30∘\widehat{BCD}=30^\circ. Tính độ dài đoạn ADAD. (làm tròn kết quả đến hàng phần mười)

Trả lời:

Câu 18 (1đ):

Tìm giá trị mm nhỏ nhất để hàm số y=m−2sin⁡xy=\sqrt{m-2\sin x} xác định trên R\mathbb{R}.

Trả lời:

Câu 19 (1đ):

Tính tổng các nghiệm nguyên thuộc [−2 021 ; 2 021]\Big[ -2 \, 021\,;\,2 \, 021 \Big] của phương trình cos⁡[π3(2x−4x2+8x+20)]=1\cos \Big[ \dfrac{\pi }{3}\left(2x-\sqrt{4{{x}^{2}}+8x+20} \right) \Big]=1.

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP