(x-1)(x+7)=(1-x)(3-2x)
giúp em câu này với ạ😭
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{5}\cdot x+\dfrac{x}{\sqrt{5}}=3\sqrt{5}+5\)
=>\(\dfrac{5x+x}{\sqrt{5}}=3\sqrt{5}+5\)
=>\(6x=\sqrt{5}\left(3\sqrt{5}+5\right)=15+5\sqrt{5}\)
=>\(x=\dfrac{15+5\sqrt{5}}{6}\)

a. Ta có: ˆBEH=90∘𝐵𝐸𝐻^=90∘(góc nội tiếp chắn nửa (BH)) ⇒ HE ⊥ AB
∆AHB vông tại H, đường cao HE:
AE.AB = AH2(1)𝐴𝐻2(1)
ˆHFC=90∘𝐻𝐹𝐶^=90∘(góc nội tiếp chắn nửa (HC)) ⇒ HF ⊥ AC
∆AHC vuông tại H, đường cao HF: AF.AC = AH2𝐴𝐻2(2)
Từ (1) và (2) ⇒ AE.AB = AF.AC
b. Ta có: ˆBAC=90∘𝐵𝐴𝐶^=90∘(góc nội tiếp chắn nửa (BC)) ⇒ˆEAF=90∘⇒𝐸𝐴𝐹^=90∘
Mà ˆAEH=90∘(HE⊥AB)𝐴𝐸𝐻^=90∘(𝐻𝐸⊥𝐴𝐵) và ˆAFH=90∘(HF⊥AC)𝐴𝐹𝐻^=90∘(𝐻𝐹⊥𝐴𝐶)
⇒ Tứ giác AEHF là hình chữ nhật ⇒ Tứ giác AEHF nội tiếp
ˆHEF=ˆHAF𝐻𝐸𝐹^=𝐻𝐴𝐹^(Cùng chắn cung HF của (AEHF))
ˆHAF=ˆABC⇒𝐻𝐴𝐹^=𝐴𝐵𝐶^⇒ EF là tiếp tuyến (BH)
c. Ta sẽ chứng minh ˆAIH=ˆKAC𝐴𝐼𝐻^=𝐾𝐴𝐶^
Ta có: ˆKAC=ˆHAC𝐾𝐴𝐶^=𝐻𝐴𝐶^ (tính chất đối xứng)
ˆHAC=ˆAHE𝐻𝐴𝐶^=𝐴𝐻𝐸^ (so le trong) ⇒ˆKAC=ˆAHE⇒𝐾𝐴𝐶^=𝐴𝐻𝐸^
ˆAIH=ˆAHE𝐴𝐼𝐻^=𝐴𝐻𝐸^ (tính chất đối xứng)
Vậy ˆAIH=ˆKAC𝐴𝐼𝐻^=𝐾𝐴𝐶^ (Cùng = ˆAHE𝐴𝐻𝐸^)
Mà AC // IH (tứ giác AEHF là hình chữ nhật)
⇒ˆAIH⇒𝐴𝐼𝐻^ và ˆKAC𝐾𝐴𝐶^ đồng vị ⇒ I, A, K thẳng hàng
a. Ta có: ˆBEH=90∘𝐵𝐸𝐻^=90∘(góc nội tiếp chắn nửa (BH)) ⇒ HE ⊥ AB
∆AHB vông tại H, đường cao HE:
AE.AB = AH2(1)𝐴𝐻2(1)
ˆHFC=90∘𝐻𝐹𝐶^=90∘(góc nội tiếp chắn nửa (HC)) ⇒ HF ⊥ AC
∆AHC vuông tại H, đường cao HF: AF.AC = AH2𝐴𝐻2(2)
Từ (1) và (2) ⇒ AE.AB = AF.AC
b. Ta có: ˆBAC=90∘𝐵𝐴𝐶^=90∘(góc nội tiếp chắn nửa (BC)) ⇒ˆEAF=90∘⇒𝐸𝐴𝐹^=90∘
Mà ˆAEH=90∘(HE⊥AB)𝐴𝐸𝐻^=90∘(𝐻𝐸⊥𝐴𝐵) và ˆAFH=90∘(HF⊥AC)𝐴𝐹𝐻^=90∘(𝐻𝐹⊥𝐴𝐶)
⇒ Tứ giác AEHF là hình chữ nhật ⇒ Tứ giác AEHF nội tiếp
ˆHEF=ˆHAF𝐻𝐸𝐹^=𝐻𝐴𝐹^(Cùng chắn cung HF của (AEHF))
ˆHAF=ˆABC⇒𝐻𝐴𝐹^=𝐴𝐵𝐶^⇒ EF là tiếp tuyến (BH)
c. Ta sẽ chứng minh ˆAIH=ˆKAC𝐴𝐼𝐻^=𝐾𝐴𝐶^
Ta có: ˆKAC=ˆHAC𝐾𝐴𝐶^=𝐻𝐴𝐶^ (tính chất đối xứng)
ˆHAC=ˆAHE𝐻𝐴𝐶^=𝐴𝐻𝐸^ (so le trong) ⇒ˆKAC=ˆAHE⇒𝐾𝐴𝐶^=𝐴𝐻𝐸^
ˆAIH=ˆAHE𝐴𝐼𝐻^=𝐴𝐻𝐸^ (tính chất đối xứng)
Vậy ˆAIH=ˆKAC𝐴𝐼𝐻^=𝐾𝐴𝐶^ (Cùng = ˆAHE𝐴𝐻𝐸^)
Mà AC // IH (tứ giác AEHF là hình chữ nhật)
⇒ˆAIH⇒𝐴𝐼𝐻^ và ˆKAC𝐾𝐴𝐶^ đồng vị ⇒ I, A, K thẳng hàng

a: ΔOBC cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)BC
Xét tứ giác OASI có \(\widehat{OAS}+\widehat{OIS}=90^0+90^0=180^0\)
nên OASI là tứ giác nội tiếp
b: ΔOAD cân tại O
mà OS là đường cao
nên OS là phân giác của góc AOD
Xét ΔOAS và ΔODS có
OA=OD
\(\widehat{AOS}=\widehat{DOS}\)
OS chung
Do đó: ΔOAS=ΔODS
=>\(\widehat{OAS}=\widehat{ODS}\)
=>\(\widehat{ODS}=90^0\)
=>SD là tiếp tuyến của (O)

\(\left[\dfrac{a-b}{\sqrt{ab}}-\dfrac{1}{\sqrt{a}+\sqrt{b}}\left(\dfrac{a}{\sqrt{b}}-\dfrac{b}{\sqrt{a}}\right)\right]:\dfrac{\sqrt{a}-\sqrt{b}}{\sqrt{ab}}\)
\(=\left(\dfrac{a-b}{\sqrt{ab}}-\dfrac{1}{\sqrt{a}+\sqrt{b}}\cdot\dfrac{a\sqrt{a}-b\sqrt{b}}{\sqrt{ab}}\right)\cdot\dfrac{\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{\sqrt{ab}\left(a-b\right)-a\sqrt{a}+b\sqrt{b}}{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}\cdot\dfrac{\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)
\(=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)-\left(\sqrt{a}-\sqrt{b}\right)\left(a+\sqrt{ab}+b\right)}{a-b}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(a\sqrt{b}+b\sqrt{a}-a-\sqrt{ab}-b\right)}{a-b}\)
\(=\dfrac{a\sqrt{b}+b\sqrt{a}-a-\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}\)

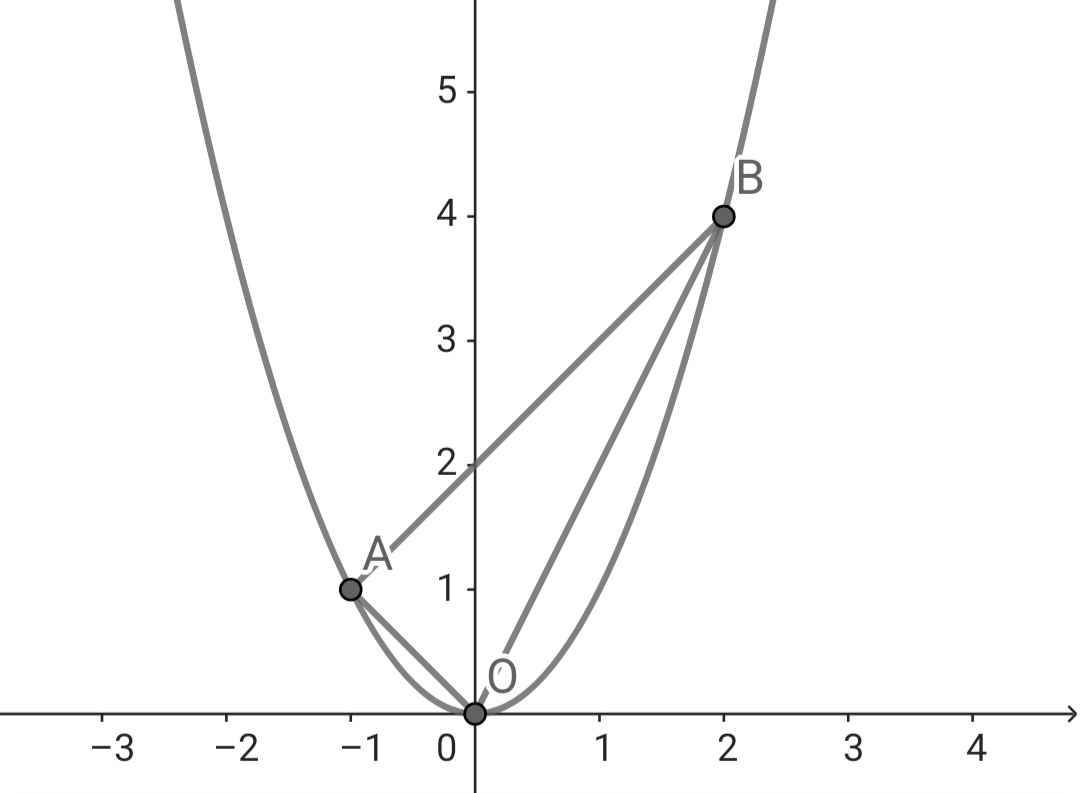
Thế x = -1 vào (P), ta có:
y = (-1)² = 1
⇒ A(-1; 1)
Thế x = 2 vào (P), ta có:
y = 2² = 4
⇒ B(2; 4)
Gọi (d): y = ax + b (a ≠ 0) là phương trình đường thẳng AB
Thế tọa độ điểm A(-1; 1) vào (d), ta có:
a.(-1) + b = 1
⇔ -a + b = 1
⇔ b = 1 + a (1)
Thế tọa độ điểm B(2; 4) vào (d), ta có:
a.2 + b = 4
⇔ 2a + b = 4 (2)
Thế (1) vào (2), ta có:
2a + 1 + a = 4
⇔ 3a = 4 - 1
⇔ 3a = 3
⇔ a = 3 : 3
⇔ a = 1 (nhận)
Thế a = 1 vào (1), ta có:
b = 1 + 1 = 2
⇒ (d): y = x + 2
Ta có:
OA² = 1 + 1 = 2
⇒ OA = √2
AB² = 3² + 3² = 18
⇒ AB = 3√2
OB² = 2² + 4² = 20
⇒ OB = 2√5
∆OAB có:
OB² = OA² + AB² = 20
⇒ ∆OAB vuông tại A (định lý Pythagore đảo)
Diện tích ∆OAB:
S = √2.3√2 : 2 = 3 (đvdt)

a) Chứng minh rằng tứ giác ACMO nội tiếp được trong một đường tròn.
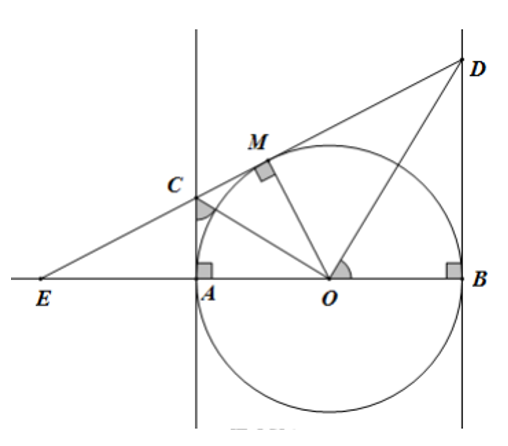
Vì AC là tiếp tuyến của (O) nên OA ⊥ AC => ˆOAC = 90o���^ = 90�
Vì MC là tiếp tuyến của (O) nên OM ⊥ MC => ˆOMC = 90o���^ = 90�
=> ˆOAC +ˆOMC =180o.���^ +���^ =180�. Suy ra OACM là tứ giác nội tiếp
Lời giải:
$(x-1)(x+7)=(1-x)(3-2x)$
$\Leftrightarrow x^2+6x-7=3-5x+2x^2$
$\Leftrightarrow x^2-11x+10=0$
$\Leftrightarrow (x-1)(x-10)=0$
$\Leftrightarrow x-1=0$ hoặc $x-10=0$
$\Leftrightarrow x=1$ hoặc $x=10$