 Giúp mk vs!!!
Giúp mk vs!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(P=\frac{xy+x+y+2}{x+y+2}=\frac{xy}{x+y+2}+1\)
Đặt \(Q=\frac{x+y+2}{xy}=\frac{1}{x}+\frac{1}{y}+\frac{2}{xy}\)
Ta có: \(4=x^2+y^2\ge2xy\Leftrightarrow xy\le2\)
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=8\Rightarrow x+y\le2\sqrt{2}\)
\(Q=\frac{1}{x}+\frac{1}{y}+\frac{2}{xy}\ge\frac{4}{x+y}+\frac{2}{xy}\ge\frac{4}{2\sqrt{2}}+\frac{2}{2}=1+\sqrt{2}\)
Suy ra \(P\le\frac{1}{1+\sqrt{2}}+1=\frac{\sqrt{2}-1}{\left(1+\sqrt{2}\right)\left(\sqrt{2}-1\right)}+1=\sqrt{2}\).
Dấu \(=\)khi \(x=y=\sqrt{2}\).
TL:
P=xy+x+y+2x+y+2 =xyx+y+2 +1
Đặt Q=x+y+2xy =1x +1y +2xy
Ta có: 4=x2+y2≥2xy⇔xy≤2
(x+y)2≤2(x2+y2)=8⇒x+y≤2√2
Q=1x +1y +2xy ≥4x+y +2xy ≥42√2 +22 =1+√2
Suy ra P≤11+√2 +1=√2−1(1+√2)(√2−1) +1=√2.
Dấu = khi x=y=√2.
^HT^

\(C=\left(\frac{a+\sqrt{a}}{\sqrt{a}+1}-\frac{\sqrt{a}-1}{a-\sqrt{a}}\right):\frac{\sqrt{a}-1}{a}\)
\(=\left(\frac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}-\frac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\frac{\sqrt{a}-1}{a}\)
\(=\left(\sqrt{a}-\frac{1}{\sqrt{a}}\right):\frac{\sqrt{a}-1}{a}=\frac{a-1}{\sqrt{a}}:\frac{\sqrt{a}-1}{a}=\frac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}}.\frac{a}{\sqrt{a}-1}\)
\(=\left(\sqrt{a}+1\right)\sqrt{a}\)
Với a > 0 , a khác 1 ta có :
\(C=\left[\frac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}-\frac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right]\cdot\frac{a}{\sqrt{a}-1}\)
\(=\left(\sqrt{a}-\frac{1}{\sqrt{a}}\right)\cdot\frac{a}{\sqrt{a}-1}=\frac{a-1}{\sqrt{a}}\cdot\frac{a}{\sqrt{a}-1}=\sqrt{a}\left(\sqrt{a}+1\right)=a+\sqrt{a}\)
*bài này làm sao ấy tìm Min không ra:v*

\(11\sqrt{\left(5-a\right)^2}=11\left|5-a\right|=11\left(5-a\right)=55-11a\left(a< 5\right)\)

ĐKXĐ : \(x\ge\frac{2}{3}\)
Ta có : \(\sqrt{x}\le\frac{x+1}{2}\)(BĐT AM-GM cho 2 số x và 1 không âm)
\(\sqrt{3x-2}\le\frac{3x-2+1}{2}=\frac{3x-1}{2}\)(BĐT AM-GM cho 2 số (3x-2) và 1 không âm)
\(\Rightarrow VT=\sqrt{x}+\sqrt{3x-2}\le\frac{x+1}{2}+\frac{3x-1}{2}=2x\left(1\right)\)
Ta lại có : \(VP=x^2+1\ge2x\left(2\right)\)(BĐT AM-GM cho 2 số \(x^2\)và 1 không âm)
Suy ra \(VT\le VP\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x=1\\3x-2=1\end{cases}\Leftrightarrow x=1}\)

(\(\sqrt{a}\)+\(\sqrt{b}\)+1) /\(\sqrt{a}+\sqrt{B}-1\).\(\sqrt{a}+\sqrt{b}+1\)=

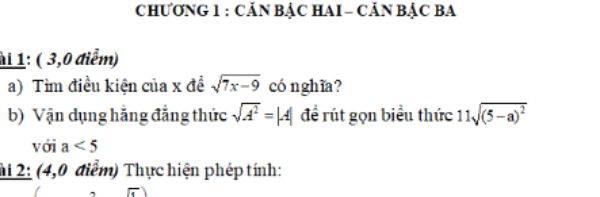
 ê ae giúp đi
ê ae giúp đi