Thứ nhất : là bài 3 bạn ghi đề bị thiếu . 

Thứ hai : là mình đã tốn thời gian giải cho bạn rồi nên đừng tiếc thời gian để k cho mình nếu mình đúng

Thứ 3 : mong các thành phần chuyên sao chép lời giải người khác và đăng lên , thậm chí là giống như đúc đừng sao chép bài của mình nhé .

Giải : 

1, Ta có : \(y\sqrt{x}-3y=\sqrt{x}+1\Rightarrow y\left(\sqrt{x}-3\right)=\sqrt{x}+1\)

\(\Rightarrow y\left(\sqrt{x}-3\right)-\left(\sqrt{x}+1\right)=0\Rightarrow y\left(\sqrt{x}-3\right)-\sqrt{x}-1=0\)

\(y\left(\sqrt{x-3}\right)-\sqrt{x}+3-4=0\Rightarrow y\left(\sqrt{x-3}\right)-\left(\sqrt{x-3}\right)-4=0\)

\(\left(\sqrt{x}-3\right)\left(y-1\right)-4=0\)

\(\left(\sqrt{x}-3\right)\left(y-1\right)=4\)

Vì y thuộc Z nên y-1 thuộc Z => \(\left(\sqrt{x}-3\right)\in Z\)

Ta có bảng : 

Vậy các cặp x,y thỏa mãn là (2;5) và (1;-1)

2,Ta có \(y\sqrt{x}-\sqrt{x}=1-y\Rightarrow\sqrt{x}\left(y-1\right)+y-1=0\Rightarrow\left(y-1\right)\left(\sqrt{x}+1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}y-1=0\\\sqrt{x}+1=0\end{cases}\Rightarrow\orbr{\begin{cases}y=1\\x\in\varnothing\end{cases}}}\)

Vậy \(y=1,x\in\varnothing\)

Không hẳn là cách khác nhưng cứ xem cho vui=)

1/\(y\left(\sqrt{x}-3\right)=\sqrt{x}+1\Leftrightarrow y=1+\frac{4}{\sqrt{x}-3}\)

Để y nguyên thì \(\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

Bài toán trở về dạng quen thuộc.

2/ \(\sqrt{x}\left(y-1\right)=1-y\)

Với y = 1 thì \(\sqrt{x}.0=0\) (luôn đúng)

Với y khác 1:

\(\sqrt{x}\left(y-1\right)=1-y\Rightarrow\sqrt{x}=\frac{1-y}{y-1}=\frac{-1\left(y-1\right)}{y-1}=-1\)(vô lí vì \(\sqrt{x}\ge0\))

Vậy x tùy ý; y = 1

3/ Thiếu đề.

Lập bảng xét dấu đi.

|x-12| + |x-14| + |x+101| + |x+990| + |x+1000| = 2017

<=> |12-x| + |14-x| + |x+101| + |x+990| + |x+1000| = 2017 >= |12-x+14-x+x+990+x+1000| + |x+101|

<=> 2017 >= 2016 + |x+101|

<=> 1>=|x+101| (1)

Mà|x+101| >=0 (2)

Từ (1) và (2) suy ra : 0<= |x+101| <= 1.

Mà x thuộc Z => x+101 = 0 hoặc x + 101 = 1.

<=> x = -101 hoặc x = 100.

Vậy x = {-101;100}

 mk vẽ hình ko đc chuẩn lắm

a,Áp dụng đ/l pytago vào tam giác vuông ABC có

AB²+AC²=BC²

9² +12²=BC²

225=BC²

=> BC = 15cm

b, Xét tam gics vuông ABC và tam giác vuông ADC có:

BA=AD (GT)

AC : cạnh chung

=> tam gics vuông ABC = tam giác vuông ADC ( 2 cạnh góc vuông)

c,ta có:tam gics vuông ABC = tam giác vuông ADC (cmt)

=> \(\widehat{BCA}=\widehat{DCA}\)(.2 góc t/ứ...)

xét tam gics vuông FAC và tam giác vuông EAC có:

\(\widehat{BCA}=\widehat{DCA}\)(CMT)

AC : cạnh chung

=>tam gics vuông FAC = tam giác vuông EAC( cạnh huyền góc nhọn)

=> CE = CF ( ...2 cạnh t/ứ.)

* , CM EF // DB

bạn chứng minh 2 tam gics CEF  và CBD cân tại C ( cái này cm dễ mà)

xog => 2 góc ở đáy của 2 tam giác = nhau r dùng đ/lí tổg 2 góc của 1 tamgiác

rồi => 2 góc đồng vị => sog sog

*, ý d bạn tự làm nhé !

bạn tự vẽ hình nha.
a) tam giác abc vuông tại a
=> BC mũ 2 = AB mũ 2 + Ac mũ 2

Hay BC mũ 2 = 9 mũ 2 + 12 mũ 2

BC mũ 2= 81+ 144

BC mũ 2= 225

=> BC = 15

b) Xét hai tam giác vuông tam giác ABC và tam giác ADC có

AC là cạnh chung

AB = AD (gt)

Do đó tam giác ABC = tam giác ADC ( 2 cạnh góc vuông )

c) Ta có tam giác ABC =  tam giác ADC ( cmt (

=> Góc BCA = góc DCA ( 2 góc tương ứng )

Xét hai tam giác vuông tam giác CFA và tam giác CEA có

AC là cạnh chung

góc C1 = góc C2 ( cmt )

Do đó tam giác CFA = tam giác CEA ( cạnh huyền -góc nhọn)

=> CE = CF ( 2 cạnh tương ứng )

Gọi N là giao điểm của EF và AC

Xét hai tam giác CFN và tam giác CEN có

CE = CF ( cmt )

C1 = C2 ( cmt )

CN là cạnh chung

Do đó tam giác CFN = tam giác CEN ( c-g-c)

=> góc CNF  = góc CNE ( 2 góc tương ứng )

mà góc CNF + góc CNE = 180 độ ( kề bù )

=> góc CNF = góc CNE = 180 độ : 2= 90 độ

=> FE vuông góc với CA

Mà CA vuông góc với BD

=> EF // DB

Cm: a) Xét t/giác ABD và t/giác AED

có AB = BE (gt)

  góc ABD = góc EBD (gt)

  BD : chung

=> t/giác ABD = t/giác AED (c.g.c)

=> AD = ED (hai cạnh tương ứng)

b) Ta có: t/giác ABD = t/giác AED (Cmt)

=> góc A = góc BED (hai góc tương ứng)

Mà góc A = 90⁰ => góc BED = 90⁰

=> DE \(\perp\)BC

 AH \(\perp\)BC

=> AH // DE (Đpcm)

c) Ta có: AH // DE (cmt)

=> góc AHD = góc HDE (so le trong)

Xét t/giác AHM và t/giác KDM 

có AH = DK (gt)

 góc AHM = góc MDC (cmt)

 HM = DM (gt)

=> t/giác AHM = t/giác KDM (c.g.c)

=> AM = KM (hai cạnh tương ứng)

=> AM \(\equiv\)MK

=> Ba điểm A, M, K thẳng hàng

Lo học đi bạn!

19 tháng 8 năm 2001

Đa thức có:

+Một nghiệm duy nhất là 7

\(3\left(x-6\right)=3\)

+Hai nghiệm là 1 và -2

\(\left(x-1\right)\left(x+2\right)=0\)

+Ba nghiệm là -1; 2 và -3

\(\left(x+1\right)\left(x-2\right)\left(x+3\right)=0\)

a, (3x²-2xy+y²) + (x²-xy+2y²) - (4x²-y²)

= 3x²-2xy+y²+x²-xy+2y²-4x²+y²

= 4y²-3xy

b, = x²-y²+2xy-x²-xy-2y²+4xy-1

= -3y²+5xy

c, M=5xy+x²-7y²+(2xy-4y)² = 5xy+x²-7y²+4x²y²-16xy²+16y² = 5xy+x²+9y²+4x²y²-16xy²

so sánh hệ tuần hoàn của lưỡng cư và bò sát

so sánh hệ tuần hoàn của bò sát và chim

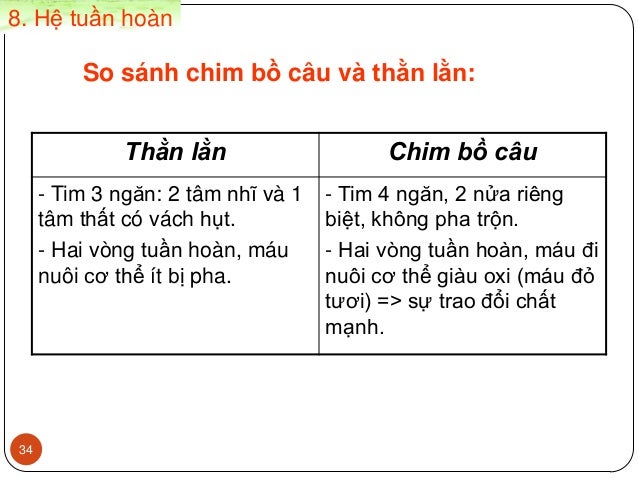
Hệ tuần hoàn của lưỡng cư (ếch) Xuất hiện vòng tuần hoàn fổi, tạo thành 2 vòng tuần hoàn với tim ba ngăn ==> máu đi nuôi cơ thể là máu pha. 
Hệ tuần hoàn của bò sát (thằn lằn):thì tim có 3 ngăn, nhưng có thêm một vách hụt ngăn tâm thất tạm thời thành 2 nửa => máu đi nuôi cơ thể ít bị fa hơn 
Hệ tuần hoàn của chim thì tim đã có 4 ngăn, gồm 2 nửa tách nhau hoàn toàn, máu đi nuôi cơ thể là máu đỏ tươi, không bị pha trộn.