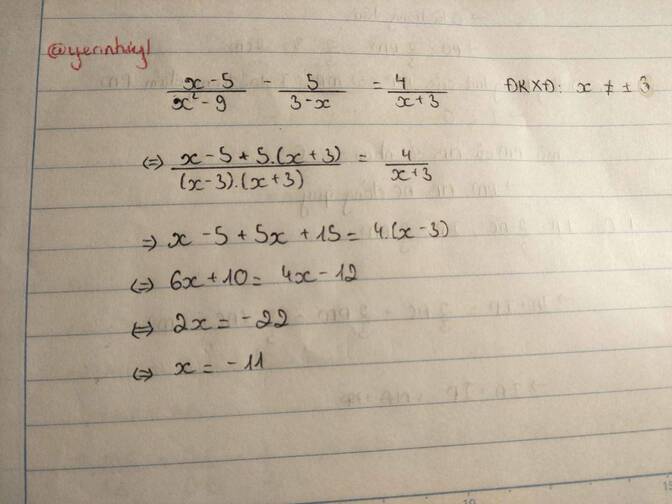chuyến xe ô to chở hành khách từ thái nguyên đi hà nội có 2 loại vé vé loại 1 giá 25000 đồng dành cho hành khách đi suốt về hà nội vế loại 2 dành cho hành khách xuống Phổ Yên giá 15000 chuyến xe đó có 38 hành khách nhà xe thu được 880000 đồng hỏi trong chuyến xe ô tô đó có bao nhiêu hành khách xuống Phổ Yên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
21 tháng 4 2022
Hiện nay tuổi mẹ là x con hiện là: x - 24
10 năm sau mẹ gấp 2 lần số tuổi hiện giờ của người con.
x+10 = 2 (x -24)
vậy mẹ hiện là 58 , con là 34.
DT
1
YN
19 tháng 6 2022
(Tớ sửa lại đề nhé.)
\(\dfrac{x-5}{x^2-9}-\dfrac{5}{3-x}=\dfrac{4}{x+3}\)
Điều kiện: \(x\ne\pm3\)
\(\Leftrightarrow\dfrac{x-5}{\left(x+3\right)\left(x-3\right)}+\dfrac{5\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{4\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}\)
\(\Rightarrow x-5+5x+15=4x-12\)
\(\Leftrightarrow x+5x-4x=-12-15+5\)
\(\Leftrightarrow2x=-22\)
\(\Leftrightarrow x=-11\)
20 tháng 4 2022
1h12p = 1,2 h
Tổng vận tốc của 2 xe là:
90 : 1,2 = 75 ( km/h )
Vận tốc của xe máy là:
( 75 - 10 ) : 2 = 32,5 ( km/h )
Vận tốc của ô tô là:
32,5 + 10 = 42,5 ( km/h )
Đ/S: Xe máy: 32,5 km/h
Ô tô: 42,5 km/h
20 tháng 4 2022
Gọi \(x\) (cây) là số cây viết màu xanh mà An đã mua \(\left(x\inℕ^∗;0< x< 10\right)\)
Vì An mua 10 cây bút xanh và đỏ nên số cây bút đỏ là \(10-x\) (cây)
Do mỗi cây viết màu xanh có giá 12 nghìn đồng nên số tiền An dành ra để mua viết xanh là \(12x\) (nghìn đồng)
Mỗi cây viết màu đỏ có giá 8 nghìn đồng nên số tiền An dành ra để mua viết đỏ là \(8\left(10-x\right)=80-8x\) (nghìn đồng)
Vì An phải trả số tiền là 96 nghìn đồng nên ta có pt
\(12x+80-8x=96\) \(\Leftrightarrow4x=16\) \(\Leftrightarrow x=4\) (nhận)
Vậy An đã mua 4 cây viết xanh và 6 cây viết đỏ.