cho tam giác ABC có ba góc nhọn,AB < AC hai đường cao BK và CI cắt nhau tại AH cắt BC tại D chứng minh tam giác ABK đồng dạng vs tam giác ACI và AK/AB=AI/AC . C/m góc AKI = góc ABC.Kéo dài KI cắt BC tại F,AD cắt KI tại Q.C/m QK.FI=FK.QI . Chứng minh KA/KC.FC/FB.IB/IA=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,3\left(x-2\right)-5=1-2x\)
\(\Leftrightarrow3x-6-5=1-2x\)
\(\Leftrightarrow5x=12\)
\(\Leftrightarrow x=\dfrac{12}{5}\)
Vậy....
\(b,\left(2x-1\right)\left(x^2+2x-3\right)=4x^2-1\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2x-3\right)=\left(2x\right)^2-1^2\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2x-3\right)=\left(2x-1\right)\left(2x+1\right)\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2x-3\right)-\left(2x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2x-3-2x+1\right)=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x^2+2\right)=0\)
... tự giải tiếp nhé, đến đây dễ r

=>(x-2021)+(x-2022)=2
<=>x-2021+x-2022=2
<=>2x-1=2
<=>2x=1/2
<=>x=??? tính nhé

Gọi quãng đường AB là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{30}{x}-\dfrac{36}{x+21}=\dfrac{15}{60}=\dfrac{1}{4}\Rightarrow x\approx32,5km\)

Đặt 4X - 19 =a; 4X -20 =b => 8X-39 = a + b
Từ đó ta có:
a^4 + b^4 = (a+b)^4 = a^4 + b^4 + 4a^3.b + 6a^2b^2 + 4ab^3
=> 4a^3.b + 6a^2.b^2 + 4a.b^3 = 0
ab(4a^2 + 6ab + 4b^2) =0
=> ab = 0 hoặc 4a^2 + 6ab +4b^2 = 0
TH1: ab = 0 -> 4x -19 =0 hoặc 4x-20 =0 => x =19/4 hoặc x = 20/4 =5
TH2: 4a^2 + 6ab +4b^2 = 0 => 2a^2 + 3ab +2b^2 = 0
Mà a - b = 1 ->a = 1+b
Thế vào ta có: 2(1+b)^2 + 3(1+b)+2b^2
= 2(1+2b+b^2) + 3b +3 + 2b^2
= 4b^2 + 7b +5
detal = 7*7 - 4*4*5 < 0 , phương trình vô nghiệm b
Vậy Phương trình ban đầu có 2 nghiệm X1 = 19/4, X2 =5

a, Xét tam giác ABC và tam giác HAC có
^BCA _ chung
^BAC = ^AHC = 900
Vậy tam giác ABC ~ tam giác HAC (g.g)
\(\dfrac{AB}{AH}=\dfrac{AC}{HC}\Rightarrow AB.HC=AC.AH\)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
Ta có \(\dfrac{AB}{AH}=\dfrac{BC}{AC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{24}{5}cm\)
\(\Rightarrow CH=\dfrac{AC.AH}{AB}=\dfrac{\dfrac{8.24}{5}}{6}=\dfrac{32}{5}cm\)

\(\left(2x+1\right)\left(3x-2-5x+6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=2\end{matrix}\right.\)

a) \(A=x^2-6x+9-9y^2\)
\(=\left(x-3\right)^2-\left(3y\right)^2\)
\(=\left(x-3-3y\right)\left(x-3+3y\right)\)
b) \(B=x^3-3x^2+3x-1+2\left(x^2-1\right)\)
\(=\left(x-1\right)^3+\left(2x+2\right)\left(x-1\right)\)
\(=\left(x-1\right)\left[\left(x-1\right)^2+2x+2\right]\)
\(=\left(x-1\right).\left(x^2+3\right)\)
a, \(A=\left(x-3\right)^2-9y^2=\left(x-3-3y\right)\left(x-3+3y\right)\)
b, \(B=\left(x-1\right)^3+2\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left[\left(x-1\right)^2+2\left(x+1\right)\right]\)
\(=\left(x-1\right)\left(x^2-2x+1+2x+2\right)=\left(x-1\right)\left(x^2+3\right)\)
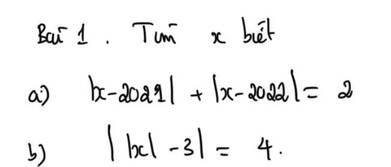
Ko trả lời thì ko đc nhắn linh tinh đâu nha!