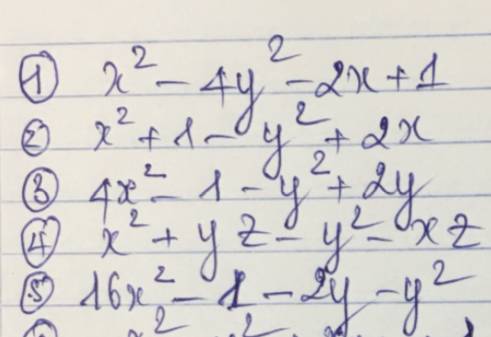Cho ABC có 3 góc nhọn (AB < AC). Gọi M , N , P lần lượt là trung điểm của các cạnh AB ,
AC , BC
a. Chứng minh từ giác BMNP là hình bình hành.
b. Kẻ đường thẳng qua B song song với MC và đường thằng qua C song song vởi AB , hai đường thằng này
cắt nhau tại D . Chứng minh P là trung điểm của đoạn thẳng MD và tứ giác MNCD là hình thang.
c. Chứng minh AP = ND
d. Tìm điều kiện của tam giác ABC dể tứ giác MNCD là hình thang cân?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\left(64x^2+22\right)-\left(4x-1\right)\left(16x^2-4x+1\right)\)
\(=64x^2+22-\left(64x^3-6x^2+4x-16x^2+4x-1\right)\)
\(=64x^2+22-\left(64x^3-22x^2+8x-1\right)\)
\(=-64x^3+86x^2-8x+23\)

\(x^2-2x+1-4y^2=\left(x-1\right)^2-\left(2y\right)^2=\left(x-1-2y\right)\left(x-1+2y\right)\)
\(x^2+2x+1-y^2=\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
\(4x^2-\left(y^2-2y+1\right)=\left(2x\right)^2-\left(y-1\right)^2=\left(2x-y+1\right)\left(2x+y-1\right)\)
\(x^2-y^2+yz-xz=\left(x-y\right)\left(x+y\right)-z\left(x-y\right)=\left(x-y\right)\left(x+y-z\right)\)
\(16x^2-\left(y^2+2y+1\right)=\left(4x\right)^2-\left(y+1\right)^2=\left(4x+y+1\right)\left(4x-y-1\right)\)