3^n+1-2x3^n + 2^n+5-7x2^n⋮25
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(313^5.299-313^6.36\)
\(=313^5.299-313^636\)
\(=313^5\left(299-313.36\right)\)
Ta có:
Ta có: \(299\equiv5\left(mod7\right)\)
\(313\equiv5\left(mod7\right)\)
\(36\equiv1\left(mod7\right)\)
=> \(299-313.36\equiv5-5.1=0\left(mod7\right)\)
=> \(299-313.36⋮7\)
=> \(313^5.299-313^6.36⋮7\)

\(A=-\dfrac{1}{3}+\dfrac{1}{3^2}-...-\dfrac{1}{3^{99}}+\dfrac{1}{3^{100}}\)
\(=\dfrac{1}{3}\left(-1+\dfrac{1}{3}\right)+\dfrac{1}{3^3}\left(-1+\dfrac{1}{3}\right)+...+\dfrac{1}{3^{99}}\left(-1+\dfrac{1}{3}\right)\)
\(=\dfrac{-2}{3}\left(\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)\)
Ta có:
\(B=\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\)
\(9B=3+\dfrac{1}{3}+...+\dfrac{1}{3^{97}}\)
\(9B-B=3-\dfrac{1}{3^{99}}\)
\(B=\dfrac{3-\dfrac{1}{3^{99}}}{8}\)
\(A=-\dfrac{2}{3}B=\dfrac{-2}{3}.\dfrac{3-\dfrac{1}{99}}{8}=\dfrac{\dfrac{1}{3^{100}}-1}{4}\)

\(\left(-0,25\right)^4\cdot4^4\)
\(=\left(-\dfrac{1}{4}\right)^4\cdot4^4\)
\(=\left(-\dfrac{1}{4}\cdot4\right)^4\)
\(=\left(-\dfrac{4}{4}\right)^4\)
\(=\left(-1\right)^4\)
\(=1\)

\(D=\dfrac{5^2}{1.6}+\dfrac{5^2}{6.11}+...+\dfrac{5^2}{26.31}\)
\(=5\left(\dfrac{5}{1.6}+\dfrac{5}{6.11}+...+\dfrac{5}{26.31}\right)\)
\(=5\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
\(=5\left(1-\dfrac{1}{31}\right)\)
\(=5.\dfrac{30}{31}=\dfrac{150}{31}\)

Lời giải:
$3,5(2)+3,5+0,0(2)=\frac{7}{2}+\frac{2}{90}=\frac{317}{90}$
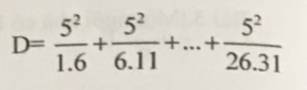
\(3^{n+1}-2.3^n+2^{n+5}-7.2^n\)
\(=3^n\left(3-2\right)+2^n\left(2^5-7\right)\)
\(=3^n+2^n.25\)
Vì \(3^n⋮̸25\); \(25.2^n⋮25\)
=> \(3^n+2^n.25⋮̸25\)
=> \(3^{n+1}-2.3^n+2^{n+5}-7.2^n⋮̸25\)