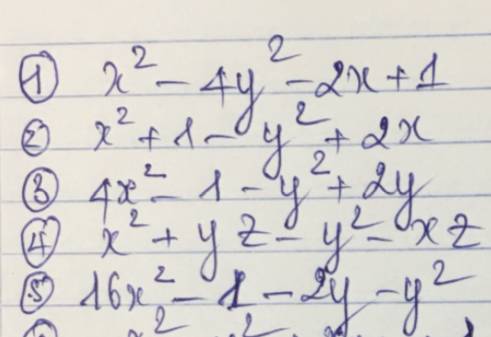Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(64x^2+22\right)-\left(4x-1\right)\left(16x^2-4x+1\right)\)
\(=64x^2+22-\left(64x^3-6x^2+4x-16x^2+4x-1\right)\)
\(=64x^2+22-\left(64x^3-22x^2+8x-1\right)\)
\(=-64x^3+86x^2-8x+23\)

\(x^2-2x+1-4y^2=\left(x-1\right)^2-\left(2y\right)^2=\left(x-1-2y\right)\left(x-1+2y\right)\)
\(x^2+2x+1-y^2=\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
\(4x^2-\left(y^2-2y+1\right)=\left(2x\right)^2-\left(y-1\right)^2=\left(2x-y+1\right)\left(2x+y-1\right)\)
\(x^2-y^2+yz-xz=\left(x-y\right)\left(x+y\right)-z\left(x-y\right)=\left(x-y\right)\left(x+y-z\right)\)
\(16x^2-\left(y^2+2y+1\right)=\left(4x\right)^2-\left(y+1\right)^2=\left(4x+y+1\right)\left(4x-y-1\right)\)


\(=x^4-x^3+x^2-\left(x^3-x^2+x\right)+x^2-x+1\)
\(=x^2\left(x^2-x+1\right)-x\left(x^2-x+1\right)+x^2-x+1\)
\(=\left(x^2-x+1\right)\left(x^2-x+1\right)\)
\(=\left(x^2-x+1\right)^2\)