Thể tích nước trong thùng ban đầu là:

\(V_1=x\cdot a\cdot b\left(dm^3\right)\)

Diện tích đáy trong thùng sau khi nghiêng là:

\(S_{đáy}=\dfrac{1}{2}\cdot\dfrac{3}{4}a\cdot8=3a\left(dm^2\right)\)

Thể tích nước sau khi nghiêng thùng là: \(V_2=3a\cdot b\left(dm^3\right)\)

Vì thể tích nước trước và sau khi nghiêng thùng đều không thay đổi nên \(x\cdot a\cdot b=3\cdot a\cdot b\)

=>x=3

Ta có; ΔABC=ΔDEF

=>AB=DE; BC=EF; AC=DF; \(\widehat{BAC}=\widehat{EDF};\widehat{ABC}=\widehat{DEF};\widehat{ACB}=\widehat{DFE}\)

Xét ΔBAM và ΔEDN có

AB=DE

\(\widehat{ABM}=\widehat{DEN}\)

BM=EN

Do đó: ΔBAM=ΔEDN

=>AM=DN và \(\widehat{BAM}=\widehat{EDN}\)

a: \(\widehat{MON}+\widehat{O_1}+45^0=180^0\)

=>\(\widehat{O_1}=180^0-90^0-45^0=45^0\)

Ta có: \(\widehat{O_1}=\widehat{MNO}\left(=45^0\right)\)

mà hai góc này là hai góc ở vị trí so le trong

nên OB//AM

b: Ta có: OB//AM

MA\(\perp\)AB

Do đó: OB\(\perp\)BA

\(A=\dfrac{1}{299}\left(1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+\dfrac{1}{3}-\dfrac{1}{302}+...+\dfrac{1}{101}-\dfrac{1}{400}\right)\)

\(299A=1+\dfrac{1}{2}+...+\dfrac{1}{101}-\left(\dfrac{1}{300}+\dfrac{1}{301}+...+\dfrac{1}{400}\right)\)

Thêm bớt \(\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{299}\) ta được:

\(299A=1+\dfrac{1}{2}+...+\dfrac{1}{101}+\left(\dfrac{1}{102}+...+\dfrac{1}{299}\right)-\left(\dfrac{1}{102}+...+\dfrac{1}{299}\right)-\left(\dfrac{1}{300}+...+\dfrac{1}{400}\right)\)

\(299A=\left(1+\dfrac{1}{2}+...+\dfrac{1}{299}\right)-\left(\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{400}\right)\)

\(101B=1-\dfrac{1}{102}+\dfrac{1}{2}-\dfrac{1}{103}+\dfrac{1}{3}-\dfrac{1}{104}+....+\dfrac{1}{299}-\dfrac{1}{400}\)

\(101B=\left(1+\dfrac{1}{2}+...+\dfrac{1}{299}\right)-\left(\dfrac{1}{102}+\dfrac{1}{103}+...+\dfrac{1}{400}\right)\)

\(\Rightarrow299A=101B\)

\(\Rightarrow\dfrac{A}{B}=\dfrac{101}{299}\)

a: m\(\perp\)a

n\(\perp\)a

Do đó: m//n

b: m//n

=>\(\widehat{A_1}=\widehat{ABC}\)(hai góc so le trong)

=>\(\widehat{A_1}=72^0\)

c: Xét ΔABC có \(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^0\)

=>\(\widehat{C_1}=180^0-64^0-72^0=44^0\)

Áp dụng công thức: \(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)

\(\Rightarrow1-\dfrac{1}{1+2+...+n}=1-\dfrac{1}{\dfrac{n\left(n+1\right)}{2}}=1-\dfrac{2}{n\left(n+1\right)}\)

\(=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)

Do đó:

\(A=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)

\(=\dfrac{1.2.3...\left(n-1\right)}{2.3.4...n}.\dfrac{4.5.6...\left(n+2\right)}{3.4.5...\left(n+1\right)}=\dfrac{1}{n}.\dfrac{n+2}{3}=\dfrac{n+2}{3n}\)

\(\Rightarrow A=\dfrac{B}{3}\)

\(\Rightarrow\dfrac{A}{B}=\dfrac{1}{3}\)

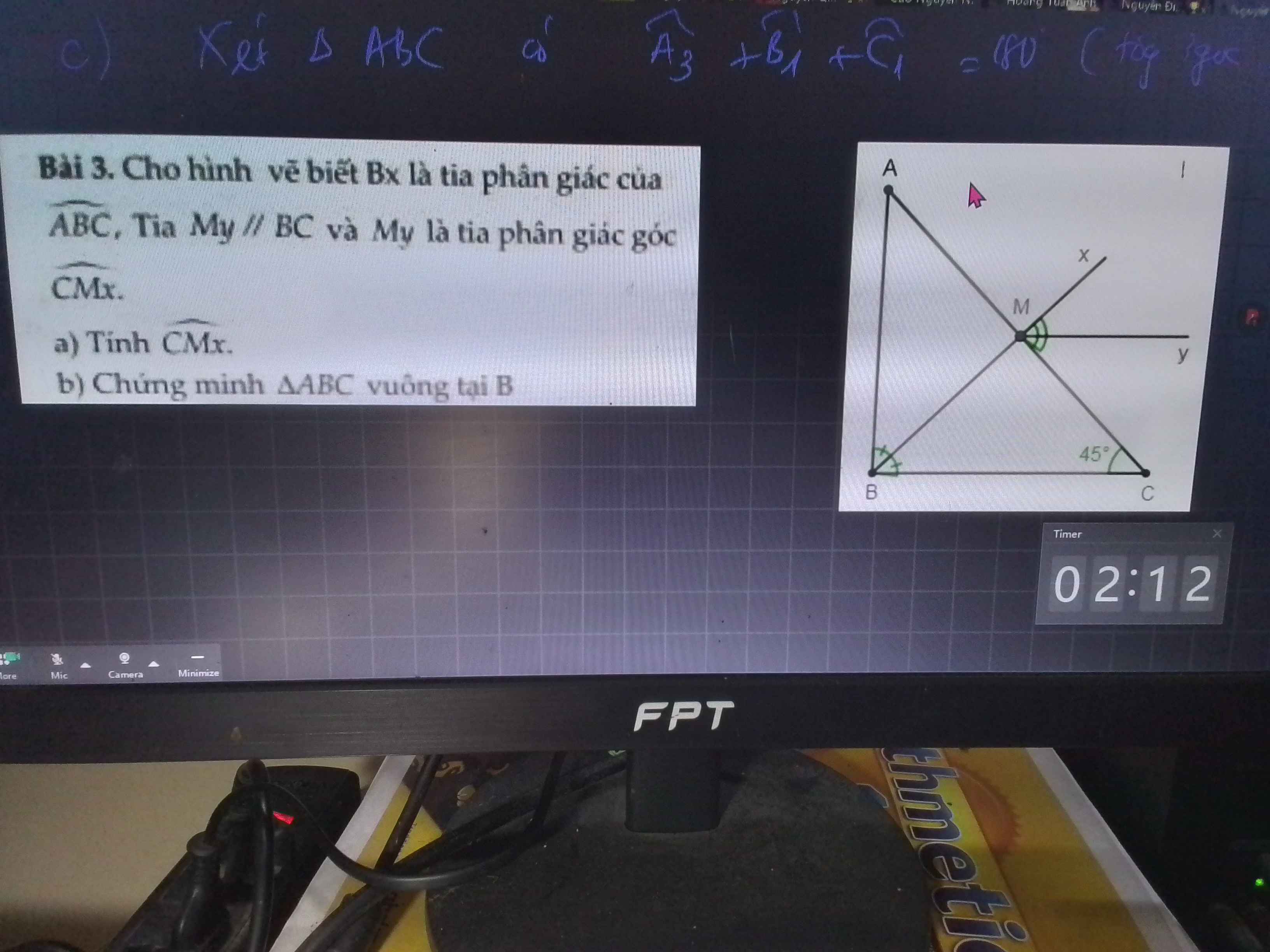
a.

Do \(My||BC\Rightarrow\widehat{CMy}=\widehat{MCB}\) (so le trong)

Mà \(\widehat{MCB}=45^0\Rightarrow\widehat{CMy}=45^0\)

lại có My là phân giác của \(\widehat{CMx}\Rightarrow\widehat{CMx}=2\widehat{CMy}\)

\(\Rightarrow\widehat{CMx}=2.45^0=90^0\)

b.

Do \(BC||My\Rightarrow\widehat{CBM}=\widehat{xMy}\)

Mà \(\widehat{xMy}=\widehat{CMy}=45^0\) (My là phân giác)

\(\Rightarrow\widehat{CBM}=45^0\)

Lại có Bx là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABC}=2\widehat{CBM}\)

\(\Rightarrow\widehat{ABC}=2.45^0=90^0\)

\(\Rightarrow\Delta ABC\) vuông tại B

\(\left(\dfrac{3}{2}\right)^5\cdot x=\left(\dfrac{3}{2}\right)^7\)

=>\(x=\left(\dfrac{3}{2}\right)^7:\left(\dfrac{3}{2}\right)^5=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)