tìm a nhỏ nhất sao cho a:5 dư 3;a;7 dư 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 12:
a:n tia chung gốc sẽ có \(\dfrac{n\left(n-1\right)}{2}\)(góc)
Theo đề, ta có: \(\dfrac{n\left(n-1\right)}{2}=28\)
=>\(n^2-n=56\)
=>\(n^2-n-56=0\)
=>(n-8)(n+7)=0
=>\(\left[{}\begin{matrix}n=8\left(nhận\right)\\n=-7\left(loại\right)\end{matrix}\right.\)
b: Theo đề, ta có: \(\dfrac{n\left(n-1\right)}{2}=190\)
=>n(n-1)=380
=>\(n^2-n-380=0\)
=>(n-20)(n+19)=0
=>\(\left[{}\begin{matrix}n=20\left(nhận\right)\\n=-19\left(loại\right)\end{matrix}\right.\)
Câu 10:
a: \(\widehat{ABC}< \widehat{BAC}< \widehat{ACB}\)
b: \(\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)

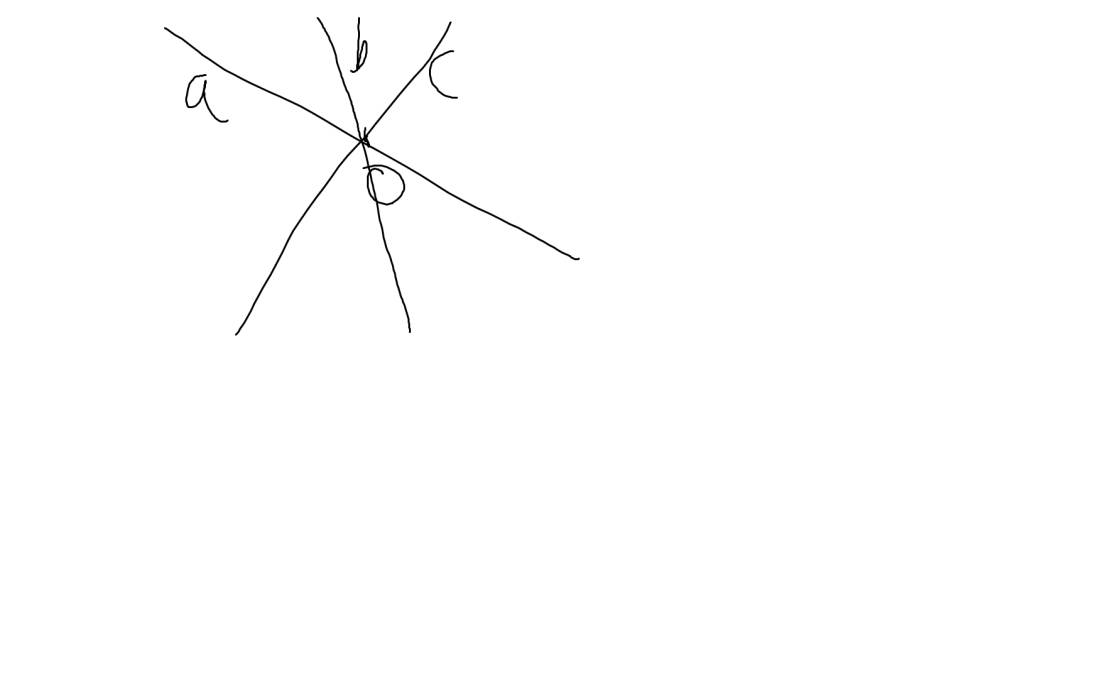
Câu 11:
a: Chúng tạo ra 13 góc
Có 3 góc bẹt
b:n đường cắt nhau sẽ có 2n tia Số góc tạo thành là \(\dfrac{2n\left(2n-1\right)}{2}=n\left(2n-1\right)\left(góc\right)\)

Câu 9:
Trên hình vẽ có 6 góc: \(\widehat{AOB};\widehat{AOC};\widehat{AOD};\widehat{BOC};\widehat{BOD};\widehat{COD}\)
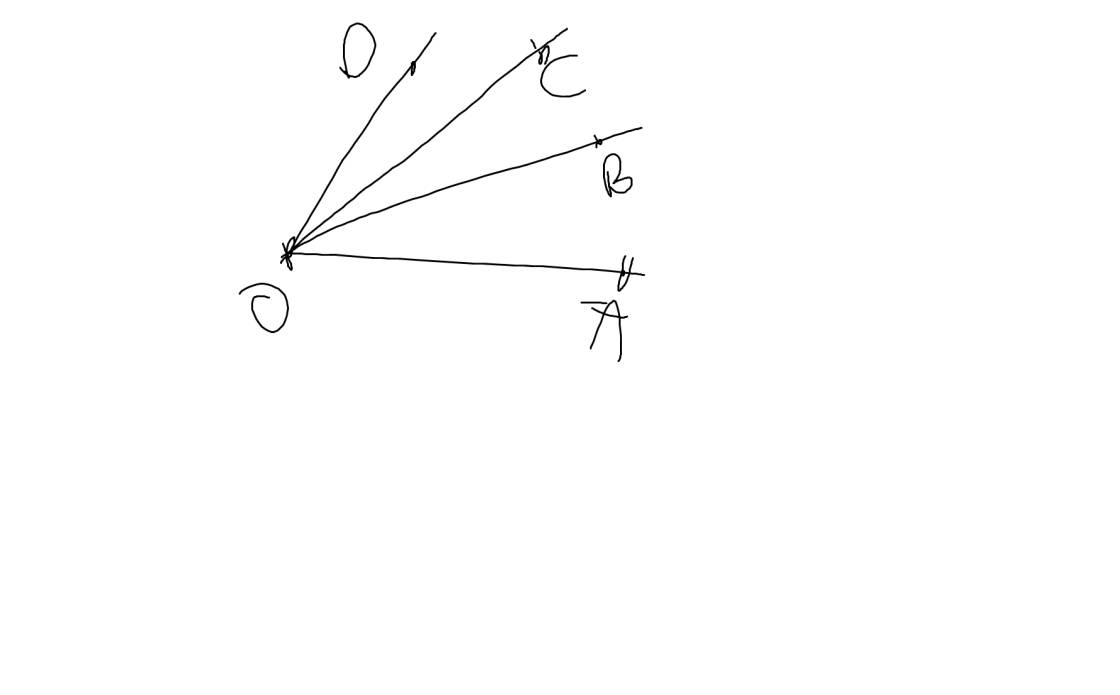

Câu 9:
Trên hình vẽ có 6 góc: \(\widehat{AOB};\widehat{AOC};\widehat{AOD};\widehat{BOC};\widehat{BOD};\widehat{COD}\)
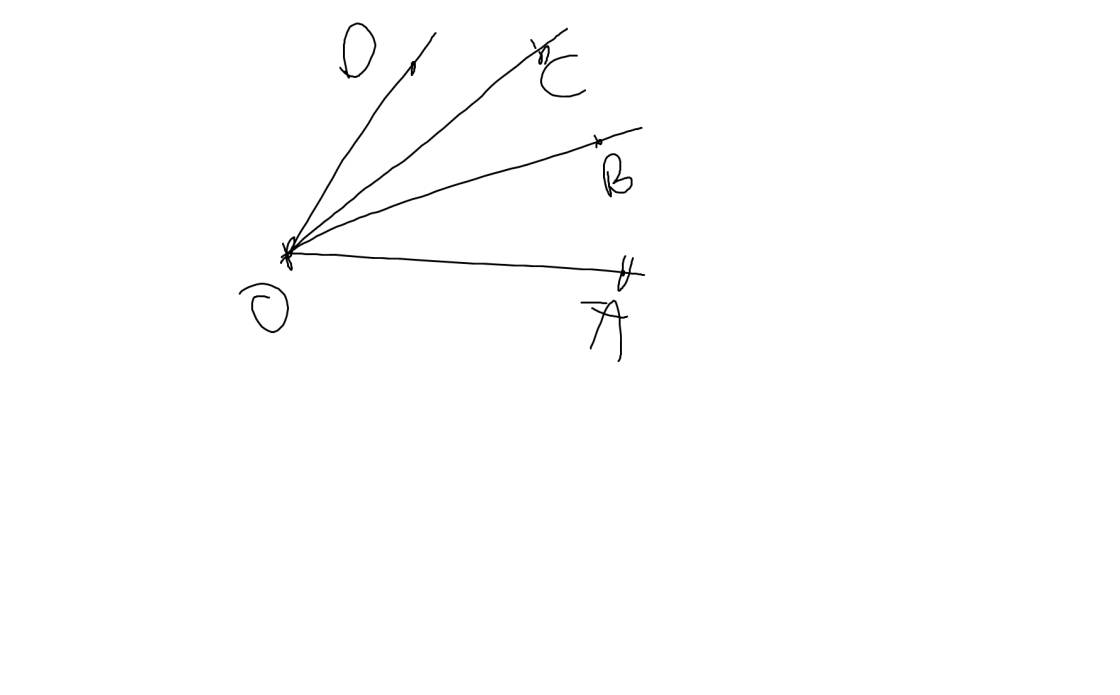
Câu 11:

xy+2y-8=4x+35
=>xy+2y-4x=43
=>y(x+2)-4x-8=35
=>(x+2)(y-4)=35
=>\(\left(x+2\right)\left(y-4\right)=1\cdot35=35\cdot1=\left(-1\right)\cdot\left(-35\right)=\left(-35\right)\cdot\left(-1\right)=5\cdot7=7\cdot5=\left(-5\right)\cdot\left(-7\right)=\left(-7\right)\cdot\left(-5\right)\)
=>\(\left(x+2;y-4\right)\in\left\{\left(1;35\right);\left(35;1\right);\left(-1;-35\right);\left(-35;-1\right);\left(5;7\right);\left(7;5\right);\left(-5;-7\right);\left(-7;-5\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(-1;39\right);\left(33;5\right);\left(-3;-31\right);\left(-37;3\right);\left(3;11\right);\left(5;9\right);\left(-7;-3\right);\left(-9;-1\right)\right\}\)

\(10A=\dfrac{10^{2022}+10}{10^{2022}+1}=1+\dfrac{9}{10^{2022}+1}\)
\(10B=\dfrac{10^{2023}+10}{10^{2023}+1}=1+\dfrac{9}{10^{2023}+1}\)
Ta có: \(10^{2022}+1< 10^{2023}+1\)
=>\(\dfrac{9}{10^{2022}+1}>\dfrac{9}{10^{2023}+1}\)
=>\(1+\dfrac{9}{10^{2022}+1}>1+\dfrac{9}{10^{2023}+1}\)
=>10A>10B
=>A>B

ĐKXĐ: n<>-1/2
Để B là số nguyên thì \(6n-8⋮2n+1\)
=>\(6n+3-11⋮2n+1\)
=>\(-11⋮2n+1\)
=>\(2n+1\in\left\{1;-1;11;-11\right\}\)
=>\(n\in\left\{0;-1;5;-6\right\}\)

ĐKXĐ: n<>7
Để A là số nguyên thì \(4n+1⋮n-7\)
=>\(4n-28+29⋮n-7\)
=>\(29⋮n-7\)
=>\(n-7\in\left\{1;-1;29;-29\right\}\)
=>\(n\in\left\{8;6;36;-22\right\}\)
theo đề ta có
a-3⋮5
a-4⋮7 (a nhỏ nhất)
=>
a-3+20⋮5
a-4+21⋮7
=>a+17⋮5
a+17⋮7
=>a+17 E BCNN(5,7)=35
=>a=35-17=18
a chia 5 dư 3 nên \(a-3\in B\left(5\right)\)
=>\(a-3\in\left\{0;5;10;15;20;...\right\}\)
=>\(a\in\left\{3;8;13;18;23;...\right\}\left(1\right)\)
a chia 7 dư 4 nên \(a-4\in B\left(7\right)\)
=>\(a-4\in\left\{0;7;14;21;...\right\}\)
=>\(a\in\left\{4;11;18;25;...\right\}\left(2\right)\)
Từ (1),(2) suy ra \(\left\{{}\begin{matrix}a\in\left\{3;8;13;18;23;...\right\}\\a\in\left\{4;11;18;25;...\right\}\end{matrix}\right.\)
mà a nhỏ nhất
nên a=18