Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhất.
Hướng dẫn: Có thể áp dụng công thức Hê-rông để tính diện tích tam giác: Nếu tam giác ABC có độ dài các cạnh là a, b, c thì diện tích của nó là: (p là nửa chu vi của tam giác.)

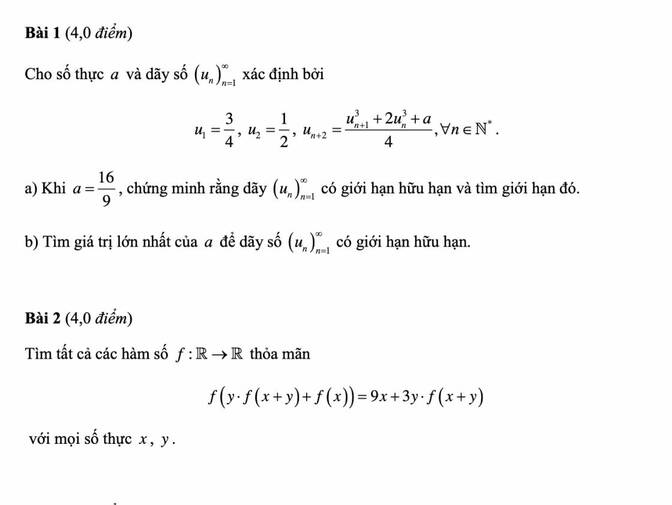


chịu :((
Gọi độ dài 2 cạnh còn lại của tam giác là x và y
\(\Rightarrow x+y+6=16\Rightarrow x+y=10\)
\(S=\sqrt{8\left(8-6\right)\left(8-x\right)\left(8-y\right)}=4\sqrt{\left(8-x\right)\left(8-y\right)}\le2\left(8-x+8-y\right)=2.6=12\)
\(S_{max}=12\) khi \(\left\{{}\begin{matrix}x+y=10\\8-x=8-y\end{matrix}\right.\) \(\Rightarrow x=y=5\)