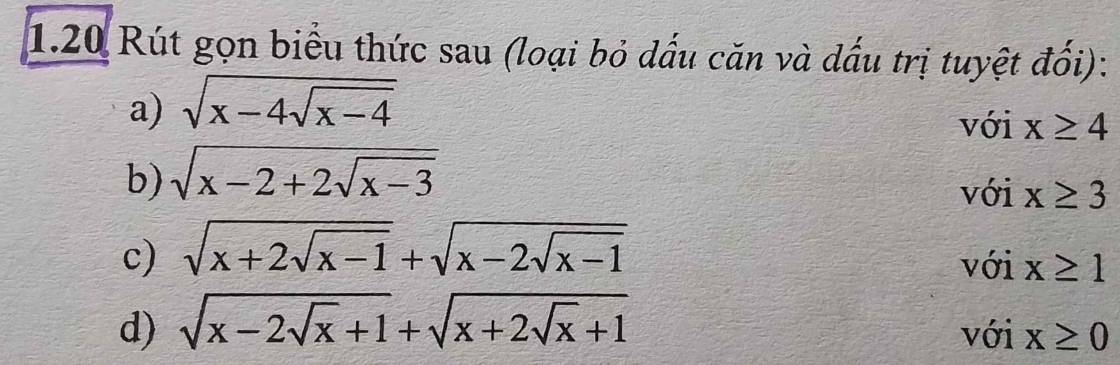 kíu tui vsssss =(((((((
kíu tui vsssss =(((((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đk x > = 2
\(x^2-3x+2=x-1\Leftrightarrow\left(x-1\right)\left(x-2\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\Leftrightarrow x=1\left(loai\right);x=3\)

Bài 2 :
Xét tam giác ABC vuông tại A
Ta có tan^B = 3/4 = AC/AB => AC = 3AB/4 = 24/4 = 6 cm
Theo định lí Pytago ta có
\(BC=\sqrt{AB^2+AC^2}=10cm\)
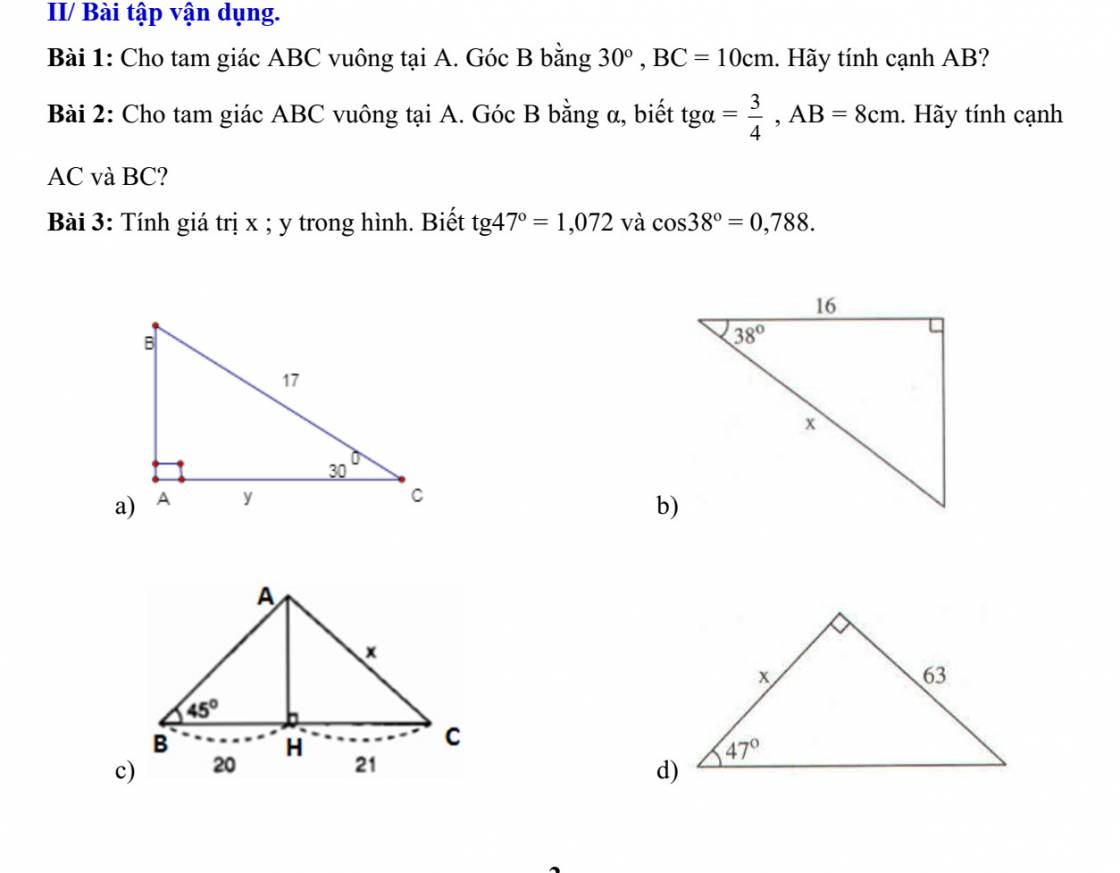
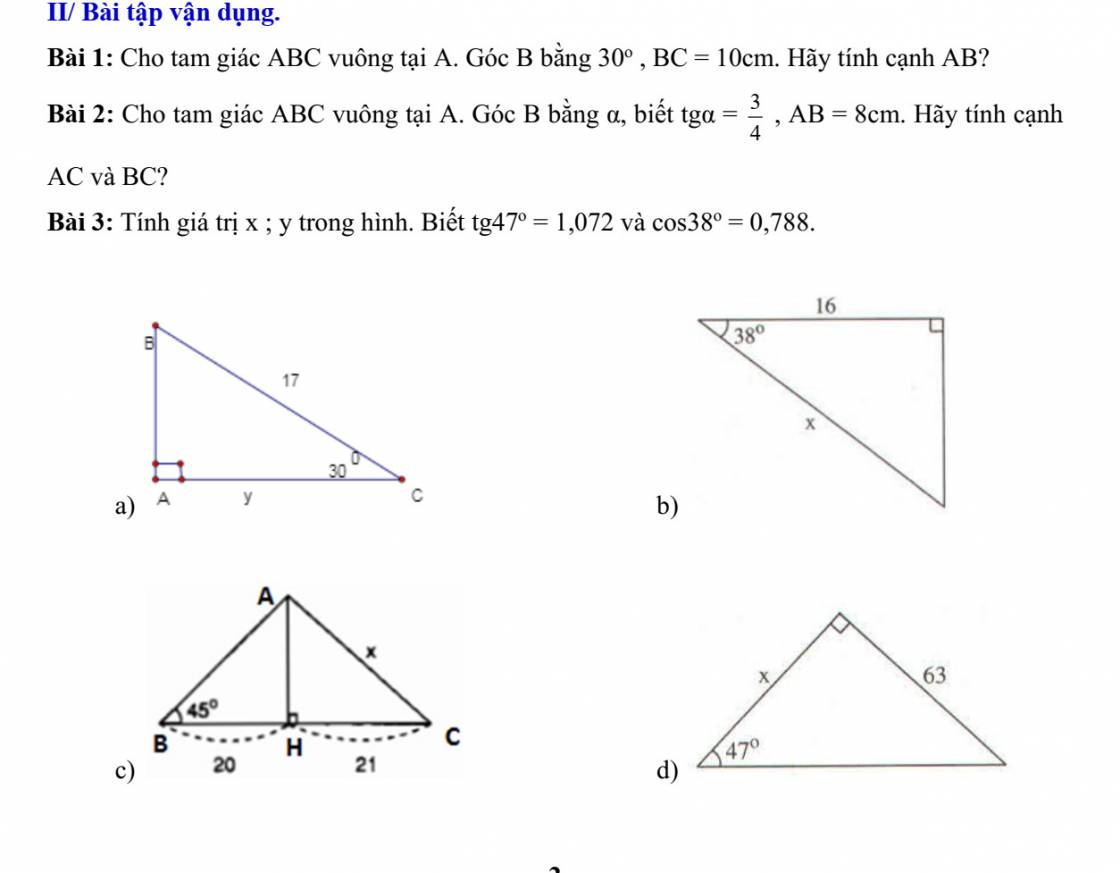
Bài 1
a, Xét tam giác ABC vuông tại A
Ta có cos^C = \(\dfrac{AC}{BC}=\dfrac{x}{17}\)
\(\Rightarrow\dfrac{\sqrt{3}}{2}=\dfrac{x}{17}\Leftrightarrow x=\dfrac{17\sqrt{3}}{2}cm\)
c, Xét tam giác AHB vuông tại H
Ta có tan^B = AH/BH
=> 1 = AH/20 <=> AH =20 cm
Theo định lí Pytago tam giacs AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=29cm\)


2D : E = | X - 9 | ( ĐKXĐ : X khác 0 )
\(\Leftrightarrow\dfrac{2\left(\sqrt{X}+3\right)}{\sqrt{X}-7}\times\dfrac{\sqrt{X}-7}{2}=\left|X-9\right|\)
\(\Leftrightarrow\sqrt{X}+3=\left|X-9\right|\)
\(\Leftrightarrow\left(\sqrt{X}+3\right)\left|\sqrt{X}-3\right|-\left(\sqrt{X}+3\right)=0\)
\(\Leftrightarrow\left|\sqrt{X}-3\right|-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{X}-3=1\\\sqrt{X}-3=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{X}=4\\\sqrt{X}=2\end{matrix}\right.\Leftrightarrow}\left[{}\begin{matrix}X=16\\X=4\end{matrix}\right.\)

a) \(\sqrt{x-4\sqrt{x-4}}=\sqrt{\left(x-4\right)-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|\)
b) \(\sqrt{x-2+2\sqrt{x-3}}=\sqrt{\left(x-3\right)+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)
\(=\sqrt{\left(x-1\right)+2\sqrt{x-1}+1}+\sqrt{\left(x-1\right)-2\sqrt{x-1}+1}\\ =\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\\ =\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|\)
d) \(\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\)
\(=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\\=\left|\sqrt{x}-1\right|+\sqrt{x}+1\)
a, đk x >= 4
\(\sqrt{x-4-4\sqrt{x-4}+4}=\sqrt{\left(\sqrt{x-4}-2\right)^2}=\left|\sqrt{x-4}-2\right|=\sqrt{x-4}-2\)
b, đk x >= 3
\(\sqrt{x-3+2\sqrt{x-3}+1}=\sqrt{\left(\sqrt{x-3}+1\right)^2}=\sqrt{x-3}+1\)
c, đk x >= 1
\(\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
\(=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)
d, tương tự