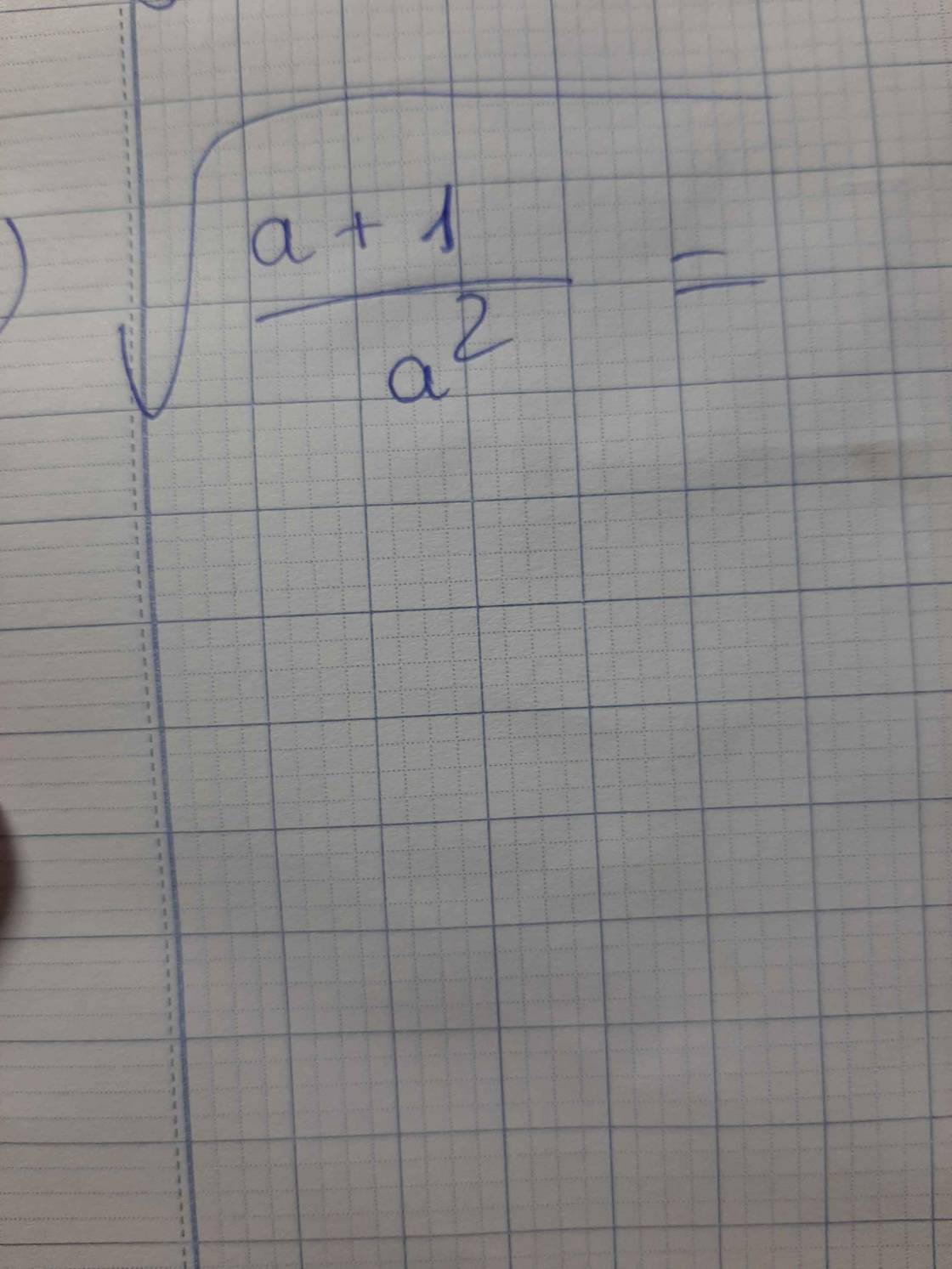 khử mẫu của biểu thức lấy căn
khử mẫu của biểu thức lấy căn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trước tiên dễ dàng tính được \(\widehat{B}=58^o\)
Tam giác ABC vuông tại A nên \(\left\{{}\begin{matrix}AB=AC.tgC\\S_{ABC}=\dfrac{1}{2}AB.AC\end{matrix}\right.\)
Mà \(\widehat{C}=32^o;S_{ABC}=80cm^2\) nên ta có \(\left\{{}\begin{matrix}AB=AC.tg32^o\\\dfrac{1}{2}AB.AC=80\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=AC.tg32^o\\AB.AC=160\end{matrix}\right.\)
Từ 2 điều này, ta có \(AC.tg32^o.AC=160\Leftrightarrow AC^2=\dfrac{160}{tg32^o}\Leftrightarrow AC=\sqrt{\dfrac{160}{tg32^o}}\) \(\approx16\left(cm\right)\)
Từ đó ta có \(AB=\dfrac{160}{AC}=\dfrac{160}{\sqrt{\dfrac{160}{tg32^o}}}\approx10\left(cm\right)\)
Cuối cùng, ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{160}{\sqrt{\dfrac{160}{tg32^o}}}\right)^2+\left(\sqrt{\dfrac{160}{tg32^o}}\right)^2}\) \(\approx18,869\left(cm\right)\)


Áp dụng định lí pytago trong tam giác vuông ABC tại A , ta có :
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow5^2+AC^2=13^2\)
\(\Leftrightarrow AC^2=13^2-5^2\)
\(\Leftrightarrow AC=\sqrt{144}=12\left(cm\right)\)
+) Xét tam giác ABC vuông tại A , đường cao AH:
\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\\AH^2=CH.BH\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5^2=BH.13\\12^2=CH.13\\AH^2=BH.CH\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{25}{13}\\CH=\dfrac{144}{13}\\AH=\sqrt{\dfrac{25}{13}.\dfrac{144}{13}}=\dfrac{60}{13}\end{matrix}\right.\)


ĐK: \(x^2-4x+4\ge0\Leftrightarrow\left(x-2\right)^2\ge0\) (luôn đúng)
\(\sqrt{x^2-4x+4}=x+2\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=x+2\\ \Leftrightarrow\left|x-2\right|=x+2\)
TH1: \(x-2\ge0\Leftrightarrow x\ge2\)
PT trở thành: \(x-2=x+2\Leftrightarrow-2=2\) (vô lí)
TH2: \(x-2< 0\Leftrightarrow x< 2\)
PT trở thành: \(2-x=x+2\Leftrightarrow2x=0\Leftrightarrow x=0\) (TM)
Vậy PT có nghiệm \(x=0\)
\(\sqrt{x^2-4x+4}=x+2\) \(ĐK: x \ge -2\)
\(<=>\sqrt{(x-2)^2}=x+2\)
`<=>|x-2|=x+2`
`@` Với `x-2 >= 0<=>x >= 2=>|x-2|=x-2` ptr có dạng:
`x-2=x+2`
`<=>0x=4` (Vô lí)
`@` Với `x-2 < 0<=>x < 2` Kết hợp đk \(=>-2 \le x < 2=>|x-2|=2-x` ptr có dạng:
`2-x=x+2`
`<=>2x=0`
`<=>x=0` (t/m)
Vậy `S=`{`0`}

Bài 6 ;mk ko chép lại đề bài nữa nhé
1, p=[1-\(\dfrac{4}{\sqrt{x}+1}+\dfrac{1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)]:\(\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{x-1}\right]:\dfrac{x-2\sqrt{x}}{x-1}\)
=\(\left[\dfrac{x-1-4\sqrt{x}+4+1}{x-1}\right]:\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-1}\)
=\(\dfrac{\left(\sqrt{x}-2\right)^2}{x-1}\times\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
=\(\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b, p=\(\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{x}=4\)
\(\Leftrightarrow x=16\)

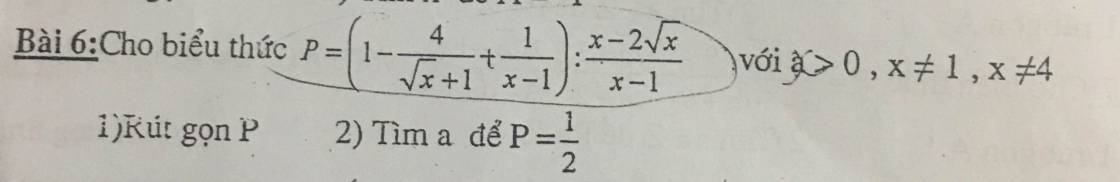
\(\dfrac{1}{a}\)\(\sqrt{a+1}\)