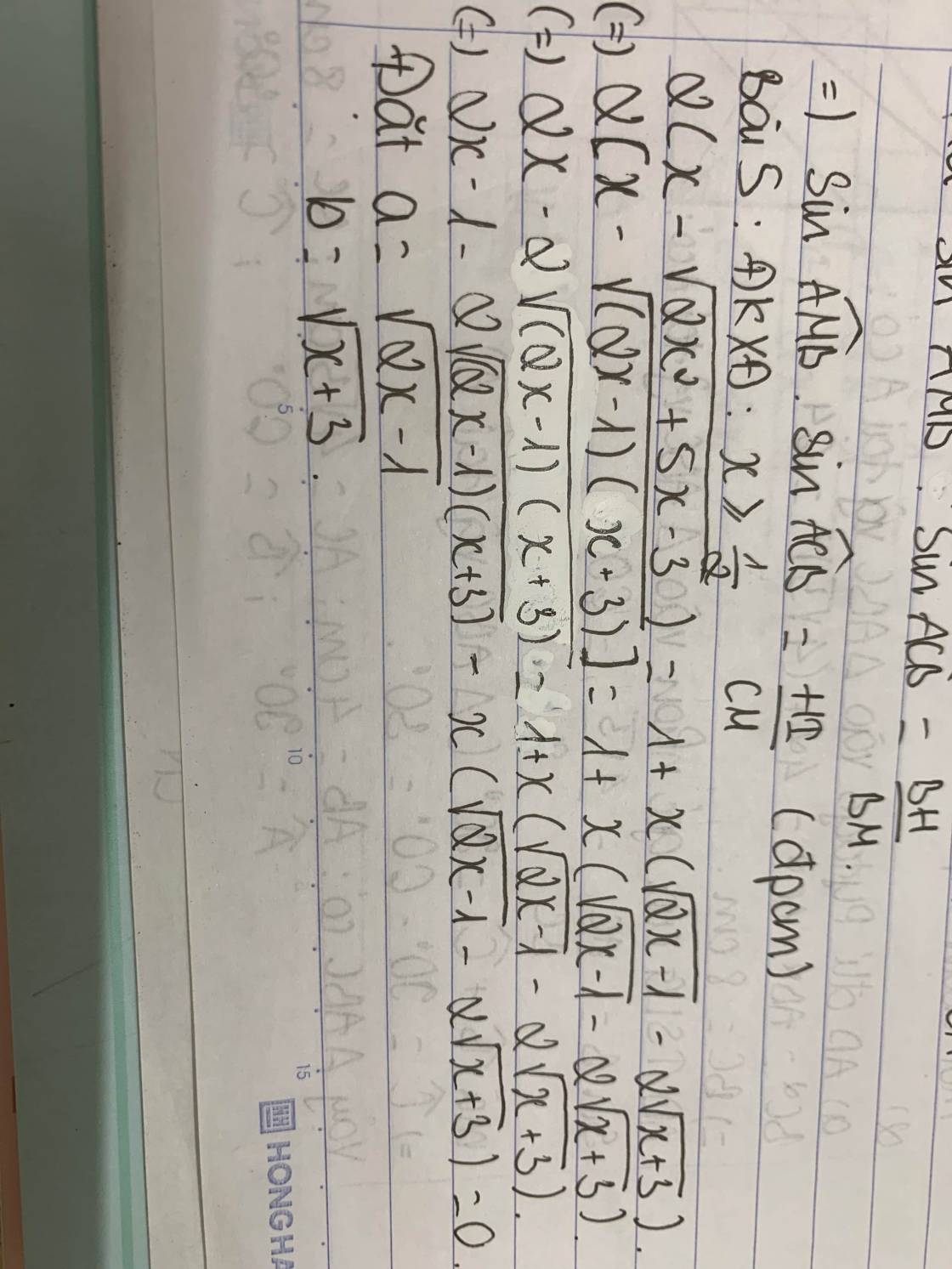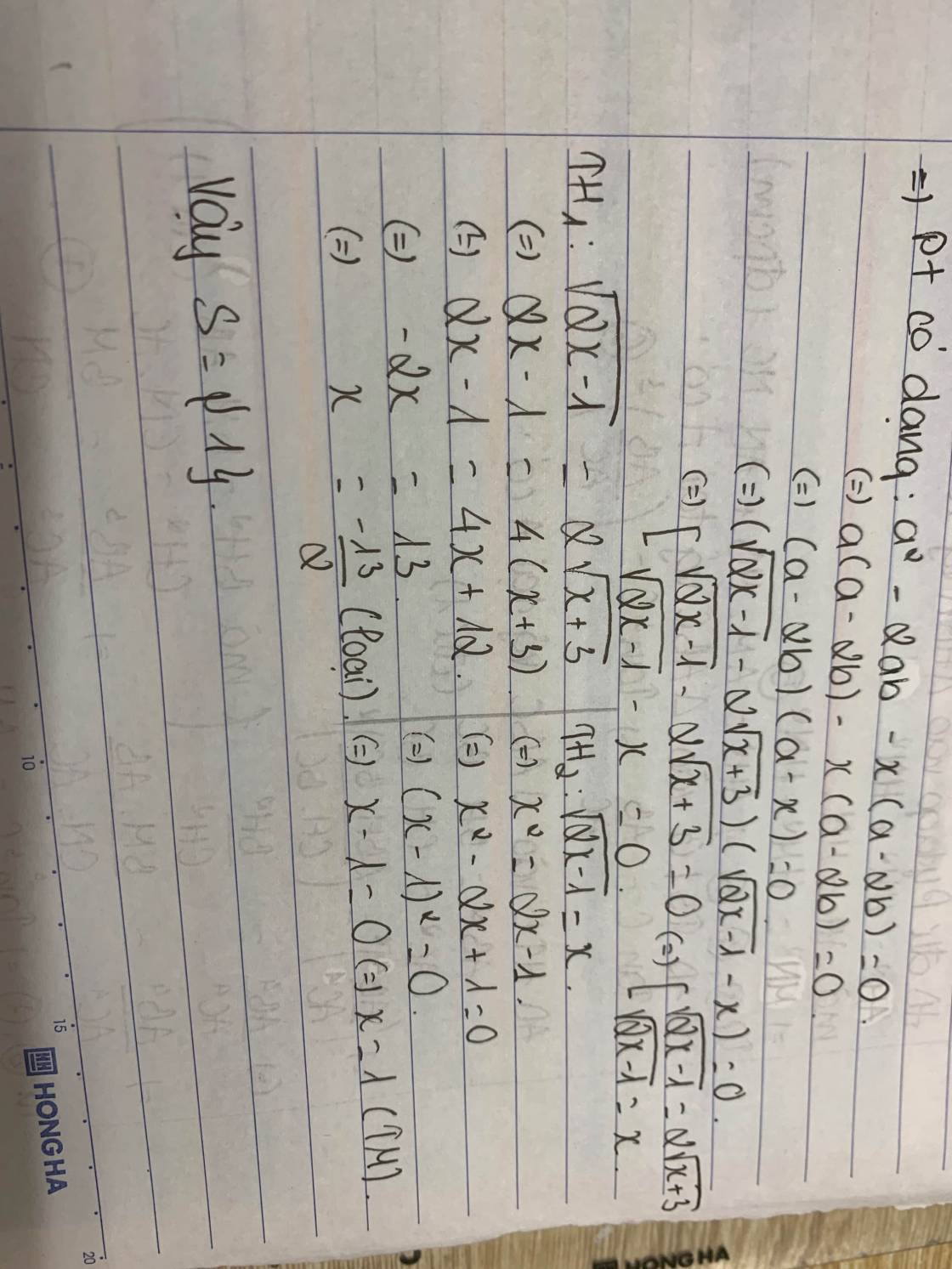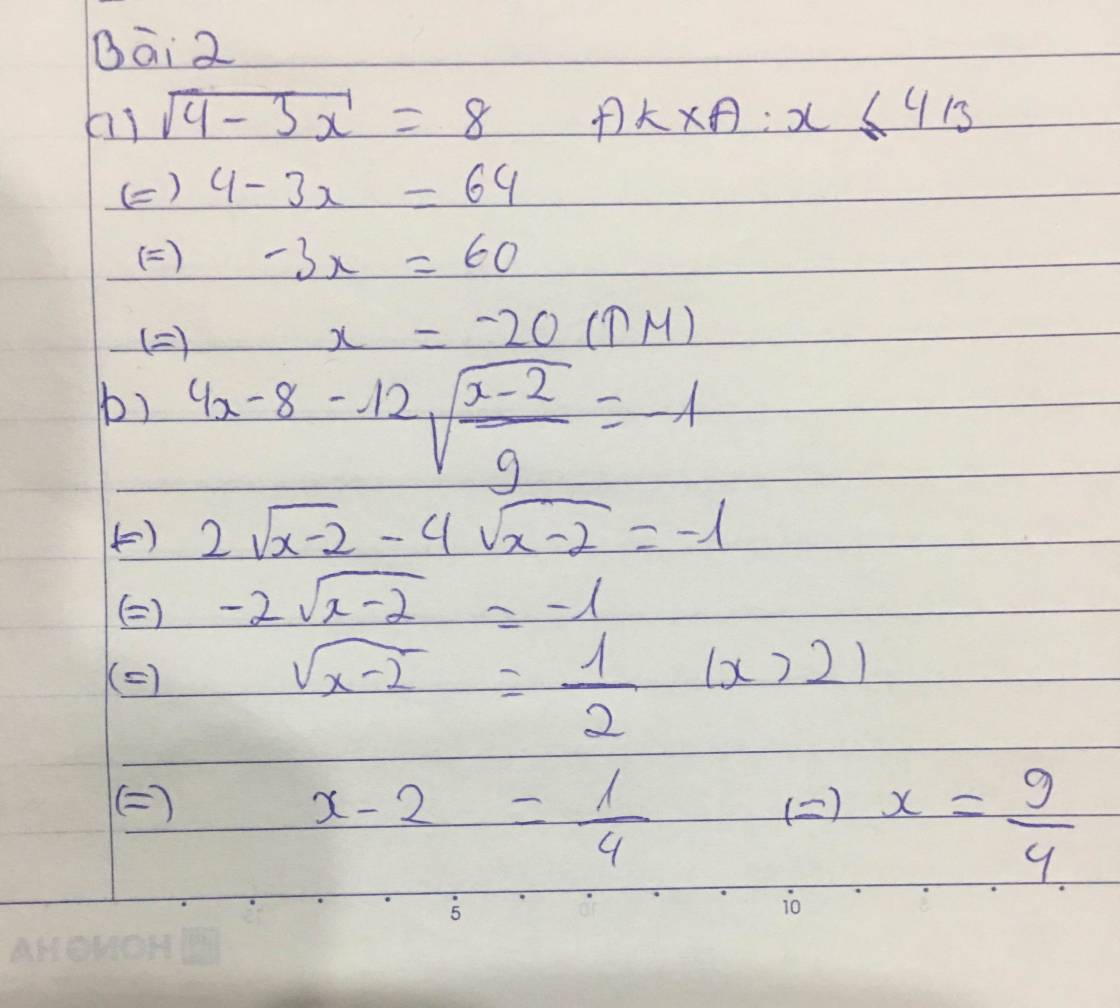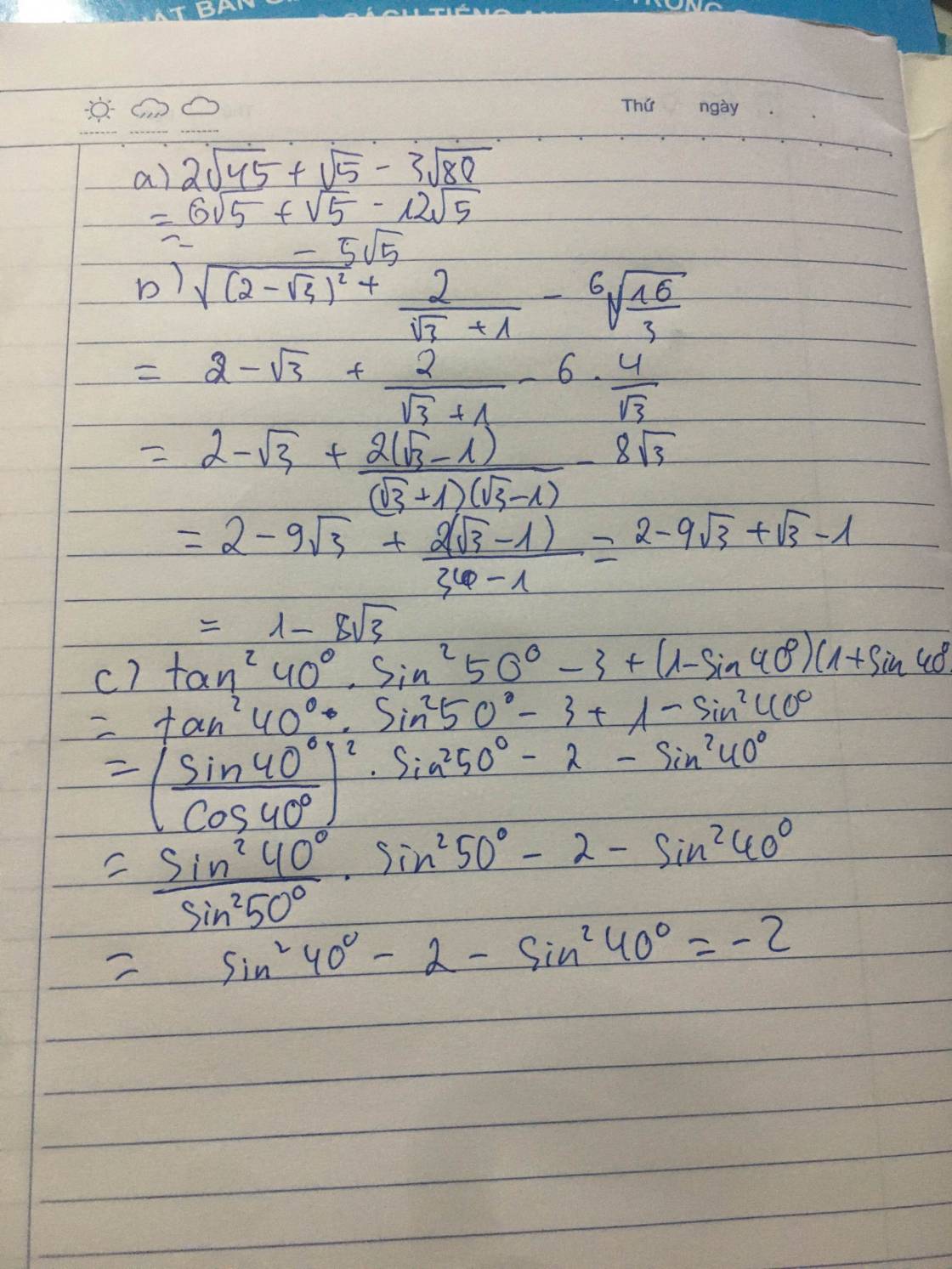Tìm nghiệm nguyên: x(x2+x+1) = 4y(y+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\sqrt{7}-\sqrt{3}\right)^2+\sqrt{84}\)
\(=10-2\sqrt{21}+2\sqrt{21}\)
= 10
Giải phương trình:
$$ 2\left(x-\sqrt{2 x^2+5 x-3}\right)=1+x(\sqrt{2 x-1}-2 \sqrt{x+3}) \text {. }$$

ĐKXĐ : \(\left\{{}\begin{matrix}2x^2+5x-3\ge0\\2x-1\ge0\\x+3\ge0\end{matrix}\right.\)
Phương trình tương đương : \(2x-2\sqrt{2x^2+5x+3}=1+x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow2x-1-2\sqrt{\left(2x-1\right)\left(x+3\right)}=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\sqrt{2x-1}.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=x.\left(\sqrt{2x-1}-2\sqrt{x+3}\right)\)
\(\Leftrightarrow\left(\sqrt{2x-1}-x\right).\left(\sqrt{2x-1}-2\sqrt{x+3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x-1}=x\\\sqrt{2x-1}=2\sqrt{x+3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{13}{2}\left(\text{loại}\right)\end{matrix}\right.\)
Vậy x = 1 là nghiệm phương trình

b ) ĐKXĐ : x ≥ 2
\(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=-1\)
\(\sqrt{4.\left(x-2\right)}-\dfrac{12}{3}\sqrt{x-2}=-1\)
\(2\sqrt{x-2}-4\sqrt{x-2}=-1\)
\(-2\sqrt{x-2}=-1\)
\(\sqrt{x-2}=\dfrac{1}{2}\)
\(\left(\sqrt{x-2}\right)^2=\left(\dfrac{1}{2}\right)^2\)
\(x-2=\dfrac{1}{4}\)
\(x=\dfrac{1}{8}\)
Vậy biểu thức vô nghiệm
a ) \(\sqrt{4-3x}=8\)
\(\left(\sqrt{4-3x}\right)^2=8^2\)
\(4-3x=8\)
\(-3x=4\)
\(x=-\dfrac{4}{3}\)

a ) \(2\sqrt{45}+\sqrt{5}-3\sqrt{80}\)
= \(2\sqrt{9.5}+\sqrt{5}-3\sqrt{16.5}\) \
= \(2.3\sqrt{5}+\sqrt{5}-3.4\sqrt{5}\)
= \(6\sqrt{5}+\sqrt{5}-12\sqrt{5}\)
= \(\left(6+1-12\right)\sqrt{5}\)
= \(-5\sqrt{5}\)
b ) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\dfrac{2}{\sqrt{3}+1}-6\sqrt{\dfrac{16}{3}}\)
= / \(2-\sqrt{3}\) / \(+\dfrac{2.\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right).\left(\sqrt{3}-1\right)}-6\sqrt{\dfrac{48}{3^2}}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{\sqrt{3}^2-1^2}-\dfrac{6}{3}\sqrt{48}\)
= \(2-\sqrt{3}+\dfrac{2.\left(\sqrt{3}-1\right)}{3-1}-2\sqrt{48}\)
=\(2-\sqrt{3}+\sqrt{3}-1-2\sqrt{16.3}\)
= \(2-\sqrt{3}+\sqrt{3}-1-8\sqrt{3}\)
= \(1-8\sqrt{3}\)
ý c ) em không biết làm ☹