giúp mình với mng ơi ai giải được thì mình xin cảm ơn nha(càng nhanh càng tốt ạ)
có 24 tờ tiền polime gồm 3 loại mệnh giá 20 nghìn đồng,50 nghìn đồng,100 nghìn đồng.trị giá mỗi loại tiền đều bằng nhau.hỏi mỗi loại có bao nhiêu tờ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

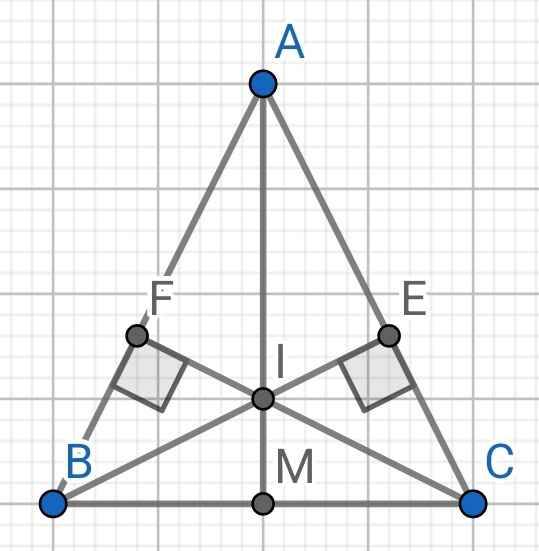
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét hai tam giác vuông: ∆ABE và ∆ACF có:
AB = AC (cmt)
∠A chung
⇒ ∆ABE = ∆ACF (cạnh huyền - góc nhọn)
b) Do ∆ABE = ∆ACF (cmt)
⇒ AE = AF (hai cạnh tương ứng)
Ta có:
BF = AB - AF
CE = AC - AE
Mà AB = AC (cmt)
AF = AE (cmt)
⇒ BF = CE
Do ∆ABE = ∆ACF (cmt)
⇒ ∠ABE = ∠ACF (hai góc tương ứng)
⇒ ∠FBI = ∠ECI
Xét hai tam giác vuông: ∆FBI và ∆ECI có:
BF = CE (cmt)
∠FBI = ∠ECI (cmt)
⇒ ∆FBI = ∆ECI (cạnh góc vuông - góc nhọn kề)
⇒ BI = IC (hai cạnh tương ứng)
⇒ ∆BIC cân tại I
c) ∆FBI vuông tại F
⇒ BI là cạnh huyền nên là cạnh lớn nhất
⇒ BI > FI
Mà BI = IC (cmt)
⇒ IC > FI
d) Do ∆ABC cân tại A (gt)
M là trung điểm của BC (gt)
⇒ AM là đường trung tuyến của ∆ABC
⇒ AM cũng là đường cao của ∆ABC
Mà I là giao điểm của hai đường cao BE và CF
⇒ A, I, M thẳng hàng


Kẻ DH//CE(H\(\in\)BC)
Ta có: DH//CE
=>\(\widehat{DHB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{DBH}\)(ΔABC cân tại A)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
mà DB=CE
nên DH=CE
Xét tứ giác DHEC có
DH//EC
DH=EC
Do đó: DHEC là hình bình hành
=>DE cắt HC tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của HC
=>H,I,C thẳng hàng
mà B,H,C thẳng hàng
nên B,I,C thẳng hàng

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó; ΔABC=ΔADC
=>CB=CD
=>ΔCBD cân tại C
b: Ta có: AD=AB
mà AB<BC(ΔABC vuông tại A)
nên AD<BC

\(x^2-5x+6=0\)
=>\(x^2-2x-3x+6=0\)
=>x(x-2)-3(x-2)=0
=>(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
=>Nghiệm của phương trình là giá trị của biến sao cho tại giá trị đó, đa thức đó có giá trị bằng 0

\(\dfrac{x-1}{3}=\dfrac{x+3}{5}\)
=>5(x-1)=3(x+3)
=>5x-5=3x+9
=>2x=14
=>x=14:2=7

a: \(\dfrac{2x-5}{x+3}=-9\)
=>-9(x+3)=2x-5
=>-9x-27=2x-5
=>-11x=22
=>\(x=-\dfrac{22}{11}=-2\)
b: Sửa đề: \(\left(x+1\right)^4=\left(x+1\right)^2\)
=>\(\left(x+1\right)^4-\left(x+1\right)^2=0\)
=>\(\left(x+1\right)^2\left[\left(x+1\right)^2-1\right]=0\)
=>\(\left(x+1\right)^2\left(x+1-1\right)\left(x+1+1\right)=0\)
=>\(x\left(x+2\right)\left(x+1\right)^2=0\)
=>\(\left[{}\begin{matrix}x=0\\x=-2\\x=-1\end{matrix}\right.\)
Tổng các số x thỏa mãn là:
0+(-2)+(-1)=-3

a: Xét ΔAMB và ΔAMC có
AB=AC
AM chung
MB=MC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
=>AM là phân giác của góc BAC
c: Xét ΔADE có AD=AE
nên ΔADE cân tại A
Ta có: ΔADE cân tại A
mà AK là đường phân giác
nên AK\(\perp\)DE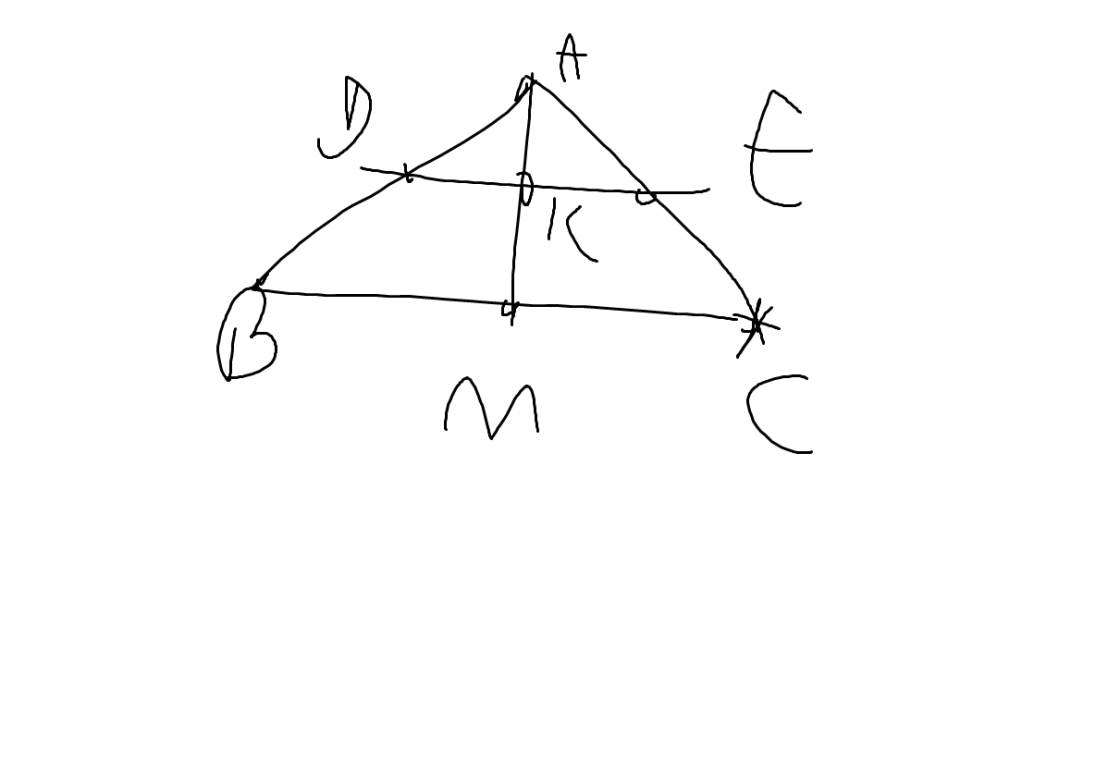
Gọi a (tờ), b (tờ), c (tờ) lần lượt là số tờ tiền polime ứng với loại 20000 đồng, 50000 đồng và 100000 đồng (a, b, c ∈ ℕ*)
Do tổng số tờ tiền là 24 tờ nên ta có:
a + b + c = 24
Do trị giá của mỗi loại tiền là như nhau nên:
20000a = 50000b = 100000c
2a = 5b = 10c
⇒ a/(1/2) = b/(1/5) = c/(1/10)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
a/(1/2) = b/(1/5) = c/(1/10) = (a + b + c)/(1/2 + 1/5 + 1/10) = 24/(4/5) = 30
2a = 30 ⇒ a = 30 : 2 = 15 (nhận)
5b = 30 ⇒ b = 30 : 5 = 6 (nhận)
10c = 30 ⇒ c = 30 : 10 = 3 (nhận)
Vậy số tờ tiền ứng với loại 20000 đồng; 50000 đồng; 10000 đồng lần lượt là: 15 tờ, 6 tờ; 3 tờ