Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ảnh thật, nhỏ hơn vật, cùng chiều với vật.
Nơi có ảnh cách thấu kính một đoạn:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{60}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ lớn ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{4}{h'}=\dfrac{60}{30}\Rightarrow h'=2cm\)

Máy phát điện xoay chiều có hai bộ phận chính:
-Nam châm.
-Cuộn dây dẫn.
Một trong hai bộ phận đó đứng yên là stato, bộ phận còn lại là roto.
Máy phát điện xoay chiều có hai bộ phận chính là nam châm và cuộn dây dẫn. Một trong hay bộ phận đó đứng yên gọi là Stato, bộ phận còn lại có thể quay được gọi là rôto.

Dòng điện cảm ứng trong cuộn dây dẫn kín đổi chiều khi số đường sức từ xuyên qua tiết diện S của cuộn dây đang tăng mà chuyển sang giảm hoặc ngược lại đang giảm mà chuyển sang tăng.
Tổng hợp 2 cách tạo ra dòng điện xoay chiều
- Cách thứ nhất: Đặt một cuộn dây dẫn quay bên trong từ trường: Cho 1 cuộn dây dẫn kín quay quanh 1 trục thẳng đứng trong từ trường của 1 nam châm.
- Cách thứ hai: Đặt nam châm quay xung quanh trước cuộn dây dẫn kín.

Nhiệt lượng m1 kg nước ở \(t_1=50^oC\) và bình nhôm tỏa ra khi hạ nhiệt độ xuống \(t_3=10^oC\) là:
\(Q_1=m_0c_{Al}\cdot\left(t_0-t_3\right)+m_1\cdot c_1\cdot\left(t_1-t_3\right)\)
\(=0,26\cdot880\cdot\left(20-10\right)+m_1\cdot4200\cdot\left(50-10\right)\)
\(=2288+168000m_1\left(J\right)\)
Nhiệt lượng m2 kg nước ở \(t_2=0^oC\) thu vào khi tăng nhiệt độ lên \(t_3=10^oC\) là:
\(Q_2=m_2\cdot c_1\cdot\left(t_3-t_2\right)=m_2\cdot4200\cdot\left(10-0\right)=42000m_2\left(J\right)\)
Cân bằng nhiệt: \(Q_1=Q_2\)
\(\Rightarrow2288+168000m_1=42000m_2\left(1\right)\)
Mà \(m_1=1,5-m_2\left(2\right)\)
Thay \(\left(2\right)\) vào \(\left(1\right)\) ta được:
\(2288+168000\left(1,5-m_2\right)=42000m_2\)
\(\Rightarrow m_2=1,21kg\)
\(\Rightarrow m_1=1,5-1,21=0,29kg\)


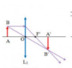
S O F F' (P') 1 A (1) (2) (3)
Vì tia sáng \(\left(1\right)\) song song với trục chính \(\Delta\) nên nó đi qua tiêu điểm ảnh \(F'\) của thấu kính hội tụ.
Vì tia sáng \(\left(2\right)\) đi qua quang tâm \(O\) nên nó truyền thẳng.
Để vẽ tia ló của tia sáng \(\left(3\right)\), ta dựng tiêu diện ảnh \(\left(P'\right)\), dựng trục phụ \(\Delta_1\) song song với tia tới \(\left(3\right)\),
gọi \(\Delta_1\) cắt \(\left(P'\right)\) tại \(A\). Khi đó, tia ló của \(\left(3\right)\) sẽ đi qua điểm \(A\).
Nhận xét: 3 tia ló trên đồng quy tại \(S'\), ảnh của điểm sáng \(S\) qua thấu kính hội tụ.

1. Chọn mẫu thiết kế nhà
Cách xây nhà cấp 4 giá rẻ hiện đại
Phương pháp tối ưu và tốt nhất để bạn có thể sở hữu mẫu nhà cấp 4 giá rẻ, trước hết đó là phải lựa chọn mẫu thiết kế nhà. Mẫu thiết kế nhà với phương án thiết kế kiến trúc hài hòa, đẹp mắt, hình khối đơn giản sẽ là lựa chọn số 1 cho bạn có một mẫu nhà tiết kiệm chi phí.
Thay vì lựa chọn một mẫu nhà đẹp cấp 4 cầu kỳ, đồ sộ, bạn có thể suy nghĩ tới cách xây nhà cấp 4 giá rẻ với mẫu thiết kế kiến trúc đơn giản, hình khối không quá cầu kỳ, nhiều chi tiết trang trí cũng như yêu cầu kỹ thuật cao.
Từ hình khối kiến trúc chúng ta có thể đi sâu phân tích cũng như đánh giá phương án thi công, từ đó có thể lên được kế hoạch dự toán chi tiết và chính xác cho công trình trước khi thi công.
2. Lựa chọn mua nguyên vật tư giá rẻ
Lựa chọn nguyên vật tư giá rẻ để có kế hoạch xây nhà giá rẻ
Lựa chọn được mẫu thiết kế nhà giá rẻ và ưng ý rồi nhưng làm sao để biến mẫu thiết kế nhà đó thành hiện thực trong thời gian sớm nhất có thể bây giờ?
Muốn xây được nhà có phương án thiết kế thi công thôi chưa đủ, bạn nên có sự chuẩn bị kỹ càng từ khâu nguyên vật tư. Để có mẫu nhà thi công giá rẻ, bạn nên chọn mua nguyên vật tư ở đâu?
Theo như kinh nghiệm của nhiều chủ đầu tư đã xây nhà trước đó cũng như nhận định của nhiều chuyên gia xây dựng trong ngành thì bạn có thể mua nguyên vật tư giá rẻ còn thừa từ những công trình lớn, không sử dụng hết, mua nguyên vật tư thanh lý giảm giá, hoặc mua nguyên vật tư của những công ty xây dựng lớn để có đơn giá chiết khấu cao. Từ đó giảm chi phí đầu tư chung cho công trình. Tuy nhiên có một điều quan trọng các bạn cần phải nhớ, mua nguyên vật tư giá rẻ nhưng phải đảm bảo chất lượng, vẫn còn hạn sử dụng và đảm bảo chất lượng khi thi công kết cấu. Tránh tình trạng ham của rẻ mà dẫn đến tình trạng công trình có chất lượng không bền vững với thời gian.
Nếu như bạn mua được nguyên vật tư giá rẻ với khối lượng lớn thì xin chúc mừng bạn, bạn đã thực hiện đúng bước thứ hai trong quy trình bí quyết cách xây nhà cấp 4 giá rẻ.
3. Lựa chọn đơn vị thi công hoặc tự thi công và giám sát thi công
Lựa chọn đơn vị thi công chuyên nghiệp để có kế hoạch xây nhà cho hợp lý
Nếu như bạn tự thi công và giám sát thi công thì bạn sẽ tiết kiệm hơn so với việc bạn lựa chọn dịch vụ trọn gói của các công ty nhà thầu chuyên nghiệp. Tuy nhiên nếu như bạn tự thi công thì bạn sẽ tốn kém nhiều thời gian, công sức cũng như phải tính toán chi tiết cẩn thận. Một đều quan trọng để đảm bảo bạn có thể thi công hoàn thiện công trình đó chính là bạn phải có sự am hiều cơ bản nhất về thi công xây dựng, nếu như không có kiến thức thì bạn không nên tự mình thi công. Tốt hơn hết bạn nên nhờ sự trợ giúp của những đơn vị thi công chuyên nghiệp.
Nếu như không có điều kiện thuê trọn gói thì bạn có thể thuê đơn vị xây dựng thi công phần thô cơ bản, cũng như phần kết cấu quan trọng, sau đó bạn tự hoàn thiện dần. Nếu như bạn tự thi công được và đảm bảo chất lượng thi công thì đây là một yếu tố quan trọng để bạn nắm vững cách xây nhà cấp 4 giá rẻ hiện nay.
4. Hoàn thiện nội thất ở mức cơ bản phù hợp với các không gian chức năng chính
Hoàn thiện nội thất ở mức cơ bản để tiết kiệm chi phí
Với phương châm cái gì cần sắm trước, cái gì chưa để sau, bạn sẽ có kế hoạch đầu tư xây nhà vô cùng hợp lý. Nếu như gia đình bạn không có điều kiện về kinh tế thì bạn chỉ nên sắm sửa những đồ nội thất cơ bản nhất, để tiết kiệm chi phí. Sau này nếu có điều kiện bạn có thể đầu tư sắm sửa sau.
Nội thất là những thứ có thể hoàn thiện dần theo không gian và theo thời gian, do đó không nhất thiết bạn phải hoàn thiện hết tất thảy trước khi hoàn thiện mẫu nhà.
Với 4 bí quyết cơ bản trên đây, nếu như nắm vững, bạn hoàn toàn có thể sở hữu được mẫu nhà giá rẻ ưng ý. 4 cách xây nhà cấp 4 giá rẻ có thể không giúp bạn sở hữu ngay mẫu nhà ưng ý, tuy nhiên có thể giúp bạn có thêm định hướng tốt và khoa học hơn cho công trình của gia đình mình trong tương lai.

Bạn tự vẽ hình nha, sgk có hướng dẫn đó, mình lười vẽ lắm.
Khoảng cách d' tới ảnh đến quang tâm O:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{20}{h'}=\dfrac{15}{30}\Rightarrow h'=40cm\)