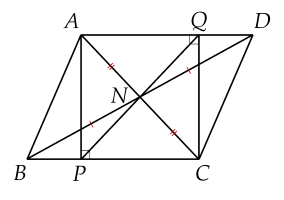
giups mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


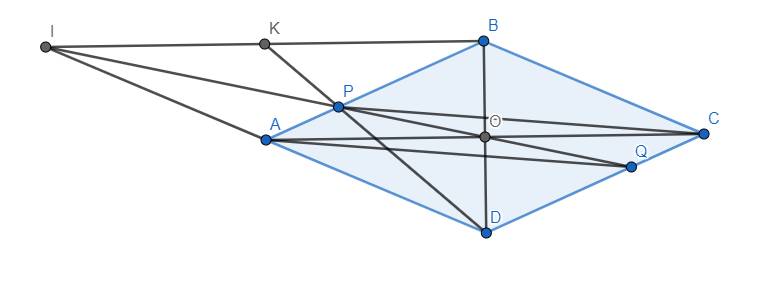
a) ABCD là hình thoi nên AB//CD và \(AB=CD\). Gọi O là giao điểm của AC và BD thì O là trung điểm của AC.
\(\Rightarrow\) AP//CQ và \(AP=\dfrac{1}{3}AB=\dfrac{1}{3}CD=CQ\) nên APCQ là hình bình hành.
Do đó PQ đi qua trung điểm O của AC.
Áp dụng định lý Menelaus cho tam giác BAD, cát tuyến IPO, ta có:
\(\dfrac{IA}{ID}.\dfrac{OD}{OB}.\dfrac{PB}{PA}=1\) \(\Rightarrow\dfrac{IA}{ID}.1.2=1\) \(\Rightarrow\dfrac{IA}{ID}=\dfrac{1}{2}\) hay A là trung điểm ID.
Từ đó dễ thấy IO là đường trung bình của tam giác DIB, suy ra BI//AO. Lại có \(AO\perp BD\) (tính chất hình thoi) nên \(BI\perp BD\), suy ra đpcm.
b) Dễ thấy P là trọng tâm tam giác BID nên K là trung điểm IB hay \(BK=IK\). Ta có đpcm.

Để nhận biết hình chữ nhật ta có bốn cách nhận biết
+ Nếu 1 tứ giác có 4 góc vuôn thì tứ giá đó là hình chữ nhật
+ Nếu 1 hình thang cân có 1 góc vuông thì hình thang cân đó là hình chữ nhật
+ Nếu hình bình hành có 1 góc vuông thì hình bình hành đó là hình chữ nhật
+ Nếu hình bình hành có hai đường chéo bằng nhau thì hình bình hành đó là hình chữ nhật
Tứ giác có ba góc vuông là hình chữ nhật. Vì tổng các góc của tứ giác là 180 độ, vì vậy khi một tứ giác có 3 góc vuông thì chúng ta có thể dễ dàng suy ra góc còn lại cũng là 90 độ. Mà tứ giác có 4 góc 90 độ thì chúng ta có thể kết luận đó là hình chữ nhật

\(-x^2+3x^2-3x+1\)
\(=-\left(x^3-3x^2+3x-1\right)\)
\(=-\left(x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3\right)\)
\(=-\left(x-1\right)^3\)
Áp dụng hằng đẳng thức số 5:
\(\left(A-B\right)^5=A^3-3A^2B+3AB^2-B^3\)

Gọi hai số đó có dạng: \(x,x+1\) (\(x\in N\))
Hiệu các bình phương của chúng là 31 nên ta có: \(\left(x+1\right)^2-x^2=31\) (1)
Giải phương trình (1) ta có:
\(\left(x+1\right)^2-x^2=31\)
\(\Leftrightarrow x^2-x^2+2x+1=31\)
\(\Leftrightarrow2x+1=31\)
\(\Leftrightarrow2x=30\)
\(\Leftrightarrow x=15\)
Vậy hai số đó là: \(15,16\)

\(C=c\left[b\left(a+d\right)\left(b-c\right)+a\left(b+d\right)\left(c-a\right)\right]+ab\left(c+d\right)\left(a-b\right)\)
\(C=c\left[\left(ab+bd\right)\left(b-c\right)+\left(ab+ad\right)\left(c-a\right)\right]+ab\left(c+d\right)\left(a-b\right)\)
\(C=c\left[ab^2-abc+b^2d-bcd+abc-a^2b+acd-a^2d\right]+ab\left(c+d\right)\left(a-b\right)\)
\(C=c\left[\left(ab^2-a^2b\right)+\left(b^2d-a^2d\right)+\left(acd-bcd\right)\right]+ab\left(c+d\right)\left(a-b\right)\)
\(C=c\left[ab\left(b-a\right)+d\left(a+b\right)\left(b-a\right)+cd\left(a-b\right)\right]+ab\left(c+d\right)\left(a-b\right)\)
\(C=c\left(a-b\right)\left(-ab-da-db+cd\right)+ab\left(c+d\right)\left(a-b\right)\)
\(C=\left(a-b\right)\left(-abc-acd-bcd+c^2d+abc+abd\right)\)
\(C=\left(a-b\right)\left(-acd-bcd+abd+c^2d\right)\)
\(C=c\left(a-b\right)\left(c^2+ab-ac-bc\right)\)
\(C=c\left(a-b\right)\left[\left(c^2-ac\right)-\left(bc-ab\right)\right]\)
\(C=c\left(a-b\right)\left[c\left(c-a\right)-b\left(c-a\right)\right]\)
\(C=c\left(a-b\right)\left(c-a\right)\left(c-b\right)\)

a: ΔABC vuông cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
AD là phân giác của góc FAE
=>AEDF là hình vuông
b: AEDF là hình vuông
=>góc AEF=45 độ
=>góc AEF=góc ABC
=>EF//BC

a) là hình chữ nhật.
b) .Tứ giác là hình thang cân
c) điều kiện của để tứ giác là hình vuông.
d)

a) là hình bình hành.
b) thẳng hàng.
c) cần thêm điều kiện gì để tứ giác là hình vuông.