Lời giải:

a. 

Ta thấy $ED\perp AB, EF\perp AC$

$\Rightarrow \widehat{EDA}=\widehat{EFA}=90^0$
Tứ giác $ADEF$ có 3 góc $\widehat{A}=\widehat{D}=\widehat{F}=90^0$ nên là hình chữ nhật.

b.

Vì $ED\perp AB, AB\perp AC\Rightarrow  ED\parallel AC$

Theo định lý Talet thì:
$\frac{BD}{DA}=\frac{BE}{EC}=1$

$\Rightarrow BD=DA$

$\Rightarrow D$ là trung điểm $AB$

Tương tự $F$ là trung điểm $AC$

$\Rightarrow DF$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$

$\Rightarrow DF\parallel BC$ và $DF=\frac{1}{2}BC$

Hay $DF\parallel BE$ và $DF=BE$

$\Rightarrow BDFE$ là hình bình hành.

Hình vẽ:

Xét tứ giác AMCD có:

ND=MN( giả thiết)

AN=NC(giả thiết)

=> tứ giác AMCD là hình bình hành

Ta có A chia hết cho B khi:

\(\dfrac{A}{B}=\dfrac{x^2y^3-2x^3y^2}{5x^2y^m}\) phải có giá trị nguyên mà \(\dfrac{A}{B}\) nguyên khi kết quả của các hạng tử đều có hạng tử có số mũ lớn hơn hoặc bằng 0 

Mà: \(\dfrac{A}{B}=\dfrac{x^2y^3-2x^3y^2}{5x^2y^m}=\dfrac{x^2y^3}{5x^2y^m}-\dfrac{2x^3y^2}{5x^2y^m}=\dfrac{1}{5}y^{3-m}-\dfrac{2}{5}xy^{2-m}\) 

Để y có số mũ lớn hơn hoạc bằng 0 thì: \(\left\{{}\begin{matrix}3-m\ge0\\2-m\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\le3\\m\le2\end{matrix}\right.\Leftrightarrow m\le2\Leftrightarrow0\le m\le2\)

Làm ơn giúp mình!!!!

Bạn cần ghi đầy đủ đề để mọi người dễ dàng hỗ trợ hơn.

a) \(\dfrac{9}{4}-3y+y^2\)

\(=\left(\dfrac{3}{2}\right)^2-3y+y^2\)

\(=y^2-2\cdot\dfrac{3}{2}\cdot y+\left(\dfrac{3}{2}\right)^2\)

\(=\left(y-\dfrac{3}{2}\right)^2\)

b) \(x^3+6x^2y+12xy^2+8y^3\)

\(=x^3+6x^2y+12xy^2+\left(2y\right)^3\)

\(=x^3+3\cdot x^2\cdot2y+3\cdot x\cdot\left(2y\right)^2+\left(2y\right)^3\)

\(=\left(x+2y\right)^2\)

 Với \(n=4\), ta chỉ ra một trường hợp sau thỏa mãn:

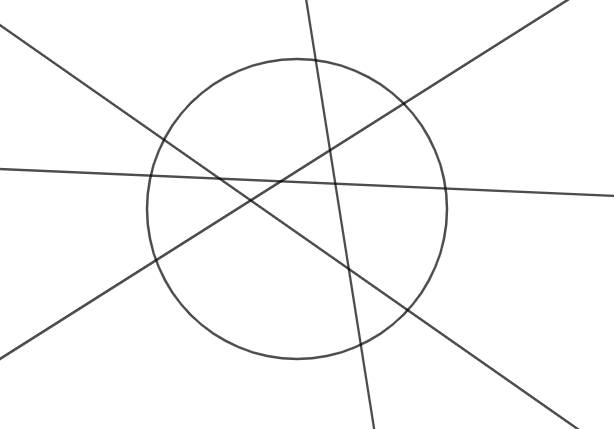
 Với \(n\le3\), ta xét trường hợp mà n đường thẳng chia hình tròn thành nhiều miền nhất. (Tức là không có 3 đường nào đồng quy và không có 2 đường thẳng nào song song hoặc cắt nhau bên ngoài hình tròn). Khi đó đường tròn bị chia thành tối đa 7 miền, không thỏa mãn.

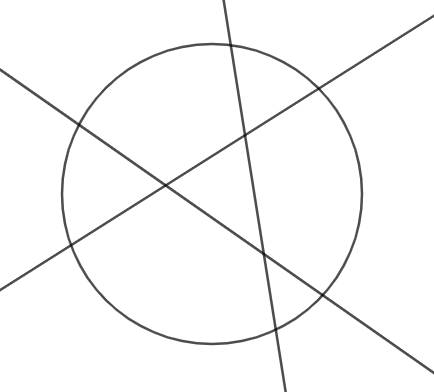
Vậy \(min_n=4\)

 Xét hệ trục tọa độ Oxy với O trùng với vị trí ban đầu của Peter, Ox trùng với hướng Tây - Đông, Oy trùng với phương Nam - Bắc.

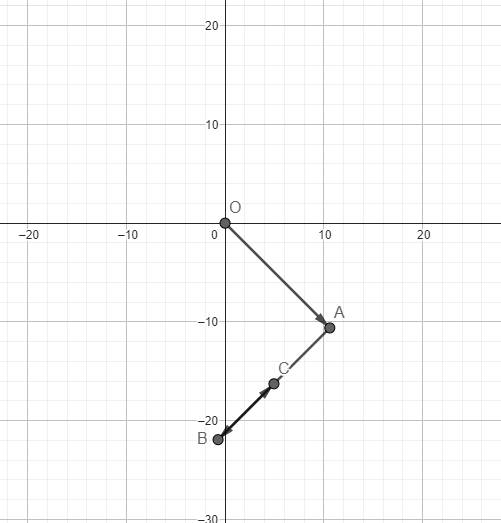
 Gọi A, B, C tương ứng là vị trí của Peter sau lần đi thứ nhất, thứ 2 và cuối cùng. 

 Ta có \(OA=16km\), \(\widehat{OAC}=90^o\) và \(AC=AB-BC=16-8=8\left(km\right)\)

 \(\Rightarrow OC=\sqrt{15^2+8^2}=17\left(km\right)\)

 Vậy sau lần đi cuối cùng, Peter cách vị trí ban đầu 17km.