
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(Q\left(2\right)=a\cdot2^2+b\cdot2+c=4a+2b+c\)
\(Q\left(-1\right)=a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=a-b+c\)
5a+b+2c=0
=>b=-5a-2c
\(Q\left(2\right)\cdot Q\left(-1\right)\)
\(=\left(4a+2b+c\right)\left(a-b+c\right)\)
\(=\left[4a+c+2\left(-5a-2c\right)\right]\left[a+c-\left(-5a-2c\right)\right]\)
\(=\left(4a+c-10a-4c\right)\left(a+c+5a+2c\right)\)
\(=\left(-6a-3c\right)\left(6a+3c\right)\)
\(=-\left(6a+3c\right)^2< =0\)

\(f\left(x\right)=x+x^5-1-x^4+x^3-x^2\)
=>\(f\left(x\right)=x^5-x^4+x^3-x^2+x-1\)
=>\(f\left(x\right)=x^4\left(x-1\right)+x^2\left(x-1\right)+\left(x-1\right)\)
=>\(f\left(x\right)=\left(x-1\right)\left(x^4+x^2+1\right)\)
Đặt f(x)=0
=>\(\left(x-1\right)\left(x^4+x^2+1\right)=0\)
mà \(x^4+x^2+1>0\forall x\)
nên x-1=0
=>x=1

\(3^2A=1-\dfrac{1}{3^2}+\dfrac{1}{3^4}-...-\dfrac{1}{3^{98}}\)
\(9A+A=1-\dfrac{1}{3^2}+\dfrac{1}{3^4}-...-\dfrac{1}{3^{98}}+\dfrac{1}{3^2}-\dfrac{1}{3^4}+\dfrac{1}{3^6}-...-\dfrac{1}{3^{100}}\)
\(10A=1-\dfrac{1}{3^{100}}\)
\(A=\dfrac{1}{10}-\dfrac{1}{10\cdot3^{100}}< 0,1\)
Vậy A<0,1

Bài 10:
\(C=\dfrac{\left|x-2017\right|+2018}{\left|x-2017\right|+2019}\)
\(=\dfrac{\left|x-2017\right|+2019-1}{\left|x-2017\right|+2019}=1-\dfrac{1}{\left|x-2017\right|+2019}\)
\(\left|x-2017\right|+2019>=2019\forall x\)
=>\(\dfrac{1}{\left|x-2017\right|+2019}< =\dfrac{1}{2019}\forall x\)
=>\(-\dfrac{1}{\left|x-2017\right|+2019}>=-\dfrac{1}{2019}\forall x\)
=>\(C=-\dfrac{1}{\left|x-2017\right|+2019}+1>=-\dfrac{1}{2019}+1=\dfrac{2018}{2019}\forall x\)
Dấu '=' xảy ra khi x-2017=0
=>x=2017

f(1)=g(2)
=>\(2\cdot1^2+a\cdot1+4=2^2-5\cdot2-b\)
=>\(a+6=-b-6\)
=>a+b=-12(1)
f(-1)=g(5)
=>\(2\cdot\left(-1\right)^2+a\cdot\left(-1\right)+4=5^2-5\cdot5-b\)
=>\(2-a+4=-b\)
=>6-a=-b
=>a-b=6(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=6\\a+b=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{-12+6}{2}=-3\\b=-12-a=-12-\left(-3\right)=-9\end{matrix}\right.\)

Ta có:
C = (3²⁰²² - 4)/3²⁰²¹
= 3.(3²⁰²² - 4)/(3.3²⁰²¹)
= (3²⁰²³ - 12)/3²⁰²²
Do 3²⁰²³ - 4 > 3²⁰²³ - 12
⇒ (3²⁰²³ - 4)/3²⁰²³ > (3²⁰²³ - 12)/3²⁰²³
⇒ B > C

Câu 4:
a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
\(\widehat{KBC}=\widehat{HCB}\)(ΔABC cân tại A)
Do đó: ΔKBC=ΔHCB
b: Ta có: ΔKBC=ΔHCB
=>\(\widehat{KCB}=\widehat{HBC}\)
=>\(\widehat{EBC}=\widehat{ECB}\)
=>ΔEBC cân tại E
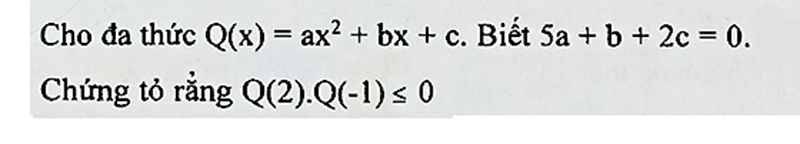
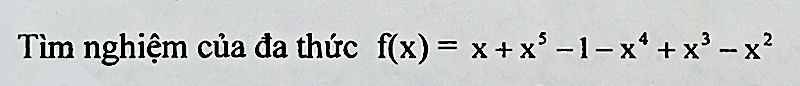
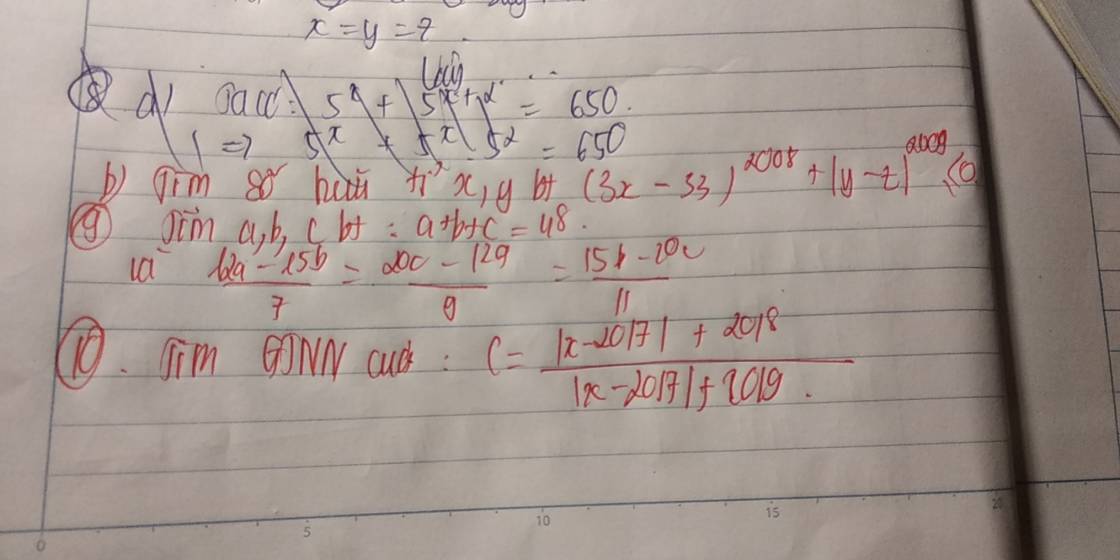

a) ∆ADE vuông tại E
⇒ AD là cạnh huyền nên là cạnh lớn nhất
⇒ AE < AD (1)
∆CDF vuông tại F
⇒ CD là cạnh huyền nên là cạnh lớn nhất
⇒ CF < CD (2)
Từ (1) và (2) ⇒ AE + CF < AD + CD
⇒ AE + CF < AC
b) Xét hai tam giác vuông: ∆ADE và ∆CDF có:
AD = CD (do D là trung điểm của AC)
∠ADE = ∠CDF (đối đỉnh)
⇒ ∆ADE = ∆CDF (cạnh huyền - góc nhọn)
⇒ AE = CF (hai cạnh tương ứng)