6,3 + (-3,7) + 2,4 + (-0,3)

= (6,3 + 2,4) + [ ( - 3,7 ) + ( - 0,3) ] 

= 8,7 +  [ - ( 3,7 + 0,3 ) ]

= 8,7 + ( - 4 )

= 4,7

a) 6,3 + ( - 3,7 ) + 2,4 + ( - 0,3 )

= 6,3 - 0,3 + 2,4 - 3,7 = 6 + 2,4 - 3,7

= 8,4 - 3,7 = 4,7

56 + 21 + 44 + 79=( 56+44)+(21+79)

                           =100+100

                           =200

56+21+44+79

=(56+44)+(21+79)

=100+100

=200

a.-5,639

b.-0,32

c.16,027

d.-2,16

Ta có EI là đường trung bình của hình thang ABCD.

Áp dụng định lý đường trung bình của hình thang ABCD ta có:

IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm )       ( 2 )

Từ ( 1 ) và ( 2 ) ta có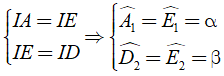 (vì trong tam giác, đối diện với hai cạn bằng

nhau là hai góc bằng nhau)

+ Xét tam giác ADE có

Ta có EI là đường trung bình của hình thang ABCD.

Áp dụng định lý đường trung bình của hình thang ABCD ta có:

IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm )       ( 2 )

Từ ( 1 ) và ( 2 ) ta có (vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)

+ Xét tam giác ADE có

1 - 12/13 = 1/13

1- 22/33 =11/33

quy đồng tử: 1/13 = 11/143

vì 11/143 < 11/33 ⇒⇒12/13 >22/33

12/13>22/33

                                     HỌC TỐT

sorry làm lại nè

\(\left(\frac{1}{2}\right)^4và\left(\frac{1}{4}\right)^4\)

ta thấy : \(\frac{1}{2}>\frac{1}{4}\Rightarrow\left(\frac{1}{2}\right)^4>\left(\frac{1}{4}\right)^4\)

Nhanh nha mọi người

a,DoΔvuông AHC có:

AH²=AE.AC (1)

Δ vuông AHB có:

AH²=AD.AB (2) 

Từ (1) và (2) :

AE.AC =AD.AB

b, Xest ΔAED và ΔABC có:

BAC^chung

AE.AC=AD.AB (câu a)

=> tam giác AED đồng dạng với tam giác ABC ( c-g-c)

a) ΔABH vuông tại H có đường cao HD

=> AD.AB = AH² (Hệ thức lượng trong tam giác vuông) (1)

ΔAHC vuông tại H có đường cao HE

=> AE.AC = AH² (Hệ thức lượng rong tam giác vuông) (2)

Từ (1) và (2) => AD.AB = AE.AC (=AH²)

câu b) bn tự làm nhé

2¹⁰+1

= 1 024 + 1

= 1 025

 vậy chữ số tận cùng của 2¹⁰+1  là 5

2¹⁰+1=2⁸x2²+1=...6x4+1=...4+1=...5

Vậy số tận cùng của 2¹⁰+1 là 5

\(\text{|}5-\frac{3}{4}x\text{|}+\text{|}\frac{2}{7}y-3\text{|}=0\)

Mà \(\text{|}5-\frac{3}{4}x\text{|}\ge0\)và \(\text{|}\frac{2}{7}y-3\text{|}\ge0\)

=>\(\hept{\begin{cases}\text{|}5-\frac{3}{4}x\text{|}=0\\\text{|}\frac{2}{7}y-3\text{|}=0\end{cases}}\)

<=>\(\hept{\begin{cases}\text{ }5-\frac{3}{4}x\text{ }=0\\\text{ }\frac{2}{7}y-3\text{ }=0\end{cases}}\)

<=>\(\hept{\begin{cases}\text{ }\frac{3}{4}x\text{ }=5\\\text{ }\frac{2}{7}y\text{ }=3\end{cases}}\)

<=>\(\hept{\begin{cases}\text{ }x\text{ }=5:\frac{3}{4}=\frac{20}{3}\\\text{ }y\text{ }=3:\frac{2}{7}=\frac{21}{2}\end{cases}}\)

\(\left|5-\frac{3}{4}x\right|+\left|\frac{2}{7}y-3\right|=0\)

\(\Rightarrow\hept{\begin{cases}5-\frac{3}{4}x=0\\\frac{2}{7}y-3=0\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x=\frac{20}{3}\\y=\frac{21}{2}\end{cases}}\)