tìm x và y biết x/6 = y/9 và x- y = 30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có: \(\frac{a}{c}\)= \(\frac{c}{b}\)\(\Rightarrow\)\(ab\)= \(c^2\)
Để chứng minh \(\frac{a^2+c^2}{b^2+c^2}\)= \(\frac{a}{b}\)thì ta phải chứng minh b(a2+c2)=a(b2+c2)
Ta có: b(a2+c2)= b.a2+b.c2 (1)
Thay ab= c2 vào 1 ta có:
b.a2+b.a.b= b2.a+a2.bb
Ta có: a(b2+c2) = a.b2+a.c2 (2)
Thay ab= c2 vào (1) ta có:
a.b2+b.a.a= b2.a+a2.bb
Vì b2.a+a2.b= b2.a+a2.b \(\Rightarrow\)b(a2+c2)= a(b2+c2)
\(\Rightarrow\)\(\frac{a^2+c^2}{b^2+c^2}\)= \(\frac{a}{b}\)
\(\Rightarrow\)Đpcm (Điều phải chứng minh)
Chúc bn học tốt
a.
\(\frac{a}{c}=\frac{c}{b}\Leftrightarrow c^2=ab\Rightarrow\frac{a^2+ab}{b^2+ab}=\frac{a.\left(a+b\right)}{b\left(a+b\right)}=\frac{a}{b}\)
b.
\(\frac{a}{c}=\frac{c}{b}\Leftrightarrow c^2=ab\Rightarrow\frac{\left(b^2-ab\right)+\left(ab-a^2\right)}{a\left(a+b\right)}=\frac{b\left(b-a\right)+a\left(b-a\right)}{a\left(a+b\right)}=\frac{b-a}{a}\)

Ta có : c/5=2c/10
Lại có a-b+2c=77
Áp dụng tính chất của dãy các tỉ số bằng nhau
Ta có a/3=b/2=2c/10=a-b+2c/3-2+10=77/11=7
=>a/3=7=>a=21
b/2=7=>b=14
2c/10=7=>c=10.7:2=35
Vậy a,b,c lần lượt là 21,14,35
Học tốt
T cho mk nhé

Ta có : x2018 + 8x2015 = 0
<=> x2015(x3 + 8) = 0
<=> \(\orbr{\begin{cases}x^{2015}=0\\x^3+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^3=\left(-2\right)^3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)
Vậy \(x\in\left\{0;-2\right\}\)là nghiệm đa thức trên

\(2\left|x+5\right|-3x=7\Leftrightarrow2\left|x+5\right|=7+3x\)
ĐK : \(x\ge-\frac{7}{3}\)
TH1 : \(2x+10=7+3x\Leftrightarrow x=3\)
TH2 : \(2x+10=-7-3x\Leftrightarrow-5x=17\Leftrightarrow x=-\frac{17}{5}\)( ktm )

\(\left|x-1\right|=2x+3\)ĐK : \(x\ge-\frac{3}{2}\)
TH1 : \(x-1=2x+3\Leftrightarrow x=-4\)( ktm )
TH2 : \(x-1=-2x-3\Leftrightarrow3x=-2\Leftrightarrow x=-\frac{2}{3}\)


|2x - 1| - |3x - 4| = 0
<=> |2x - 1| = |3x - 4|
<=> \(\orbr{\begin{cases}2x-1=3x-4\\2x-1=-3x+4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\5x=5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
Vậy \(x\in\left\{3;1\right\}\)
/2x-1/-/3x-4/=0
=>th1:2x-1=3x-4
2x-1-(3x-4)=0
2x-1-3x+4=0
2x-3x=-3
-1x=-3
x=3
th2: -2x-1=3x-4
-2x-1-(3x-4)=0
=> -2x-1-3x+4=0
-2x-3x=-3
-5x=-3
=>x=3/5
Vậy x=3;3/5

Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{15}=\frac{y}{7}=\frac{2y}{14}=\frac{x-2y}{15-14}=\frac{16}{1}=16\)
=> x = 16.15 = 240
; y = 16.7 = 112
Vậy x = 240 ; y = 112

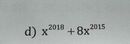
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{6}=\frac{y}{9}=\frac{x-y}{6-9}=\frac{30}{-3}=-10\)
\(\Rightarrow x=-60;y=-90\)