Thời gian: 45 phút
Bài 1: Cho ∆ABC vuông tại A, phân giác của góc B cắt AC tại D. Trên cạnh BC lấy điểm E sao cho AB = BE.
a) Chứng minh: AABD = AEBD từ đó suy ra DE vuông góc với BC.
b) Đường thẳng DE cắt đường thẳng AB tại K.Chứng minh: AADK = AEDC
c) Chứng minh: ABKC cân tại B
d) Chứng minh: BD vuông góc với CK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Ta có: \(\widehat{BMH}=\widehat{AMN}\)(hai góc đối đỉnh)
\(\widehat{CNK}=\widehat{ANM}\)(hai góc đối đỉnh)
mà \(\widehat{AMN}=\widehat{ANM}\)(ΔAMN cân tại A)
nên \(\widehat{BMH}=\widehat{CNK}\)
Xét ΔBMH vuông tại H và ΔCNK vuông tại K có
BM=CN
\(\widehat{BMH}=\widehat{CNK}\)
Do đó: ΔBMH=ΔCNK
=>BH=CK
c: Ta có: ΔBMH=ΔCNK
=>MH=NK
Ta có: AM+MH=AH
AN+NK=AK
mà AM=AN và MH=NK
nên AH=AK
Xét ΔABH và ΔACK có
AB=AC
BH=CK
AH=AK
Do đó: ΔABH=ΔACK

Câu 14: \(6z=19y\)
=>\(\dfrac{z}{19}=\dfrac{y}{6}\)
=>Chọn C

câu 13:
\(\dfrac{40x^7+25x^4-15x^2}{5x^2}=\dfrac{40x^7}{5x^2}+\dfrac{25x^4}{5x^2}-\dfrac{15x^2}{5x^2}\)
\(=8x^5+5x^2-3\)
=>Hệ số của x5 là 8
=>Chọn A

Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A

\(\left(3x-8\right)^2=5\left|3x-8\right|\)
=>\(\left(\left|3x-8\right|\right)^2=5\left|3x-8\right|\)
=>\(\left|3x-8\right|\left(\left|3x-8\right|-5\right)=0\)
=>\(\left[{}\begin{matrix}3x-8=0\\3x-8=-5\\3x-8=5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{8}{3}\\x=1\\x=\dfrac{13}{3}\end{matrix}\right.\)


a: Các biến cố chắc chắn là C
Biến cố ngẫu nhiên là D;B
Biến cố không thể là A
b: Vì A là biến cố không thể
nên P(A)=0
B: "Lấy được thẻ có số là số nguyên tố"
=>B={2}
=>n(B)=1
=>\(P\left(B\right)=\dfrac{1}{4}\)
Mọi người giải giúp mình với mình cần gấp ngày mai mình hộp bài rồi


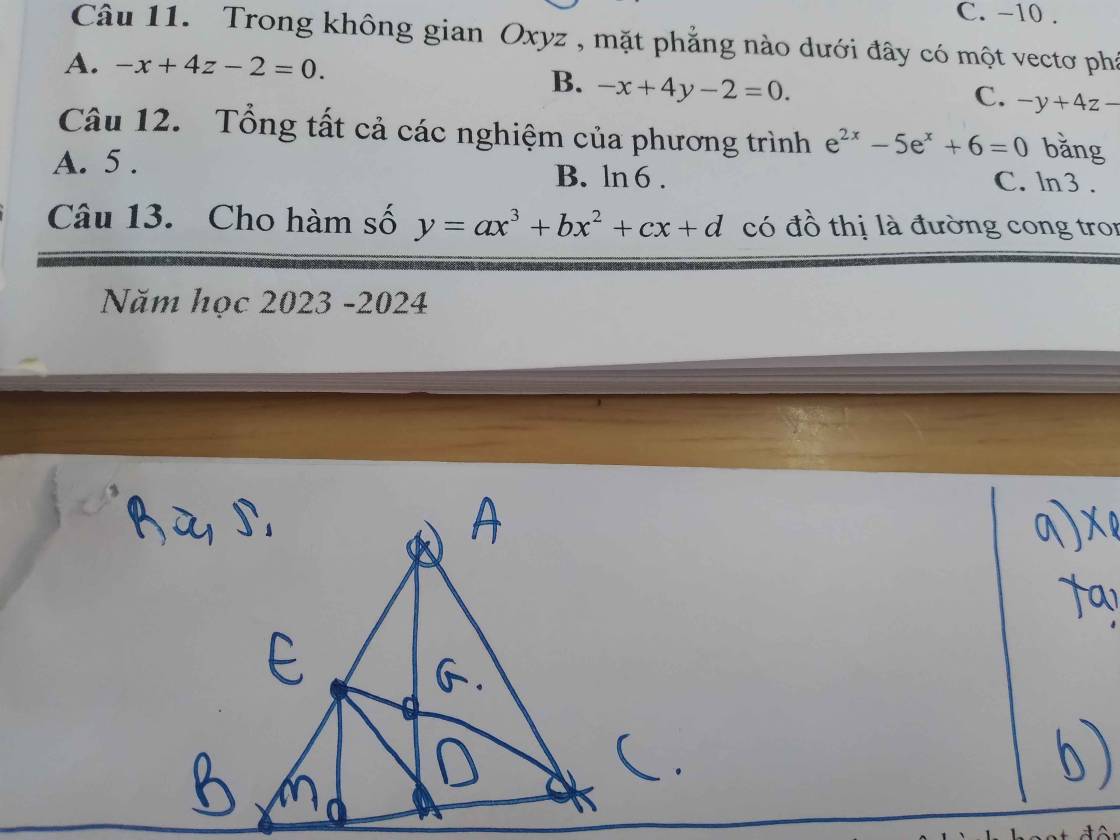
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
=>\(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó:ΔADK=ΔEDC
c: Ta có: ΔADK=ΔEDC
=>AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>ΔBKC cân tại B
d: Xét ΔBKC có
CA,KE là các đường cao
CA cắt KE tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC