\(\left(2x\right)^2.\left(x-x^2\right)-4x.\left(-x^3+x^2-5\right)=20\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
b: Ta có: ΔBAD=ΔBMD
=>DA=DM
mà DM<DC(ΔDMC vuông tại M)
nên DA<DC
c: Xét ΔBKC có
KM,CA là các đường cao
KM cắt CA tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC tại N
Sửa đề: ΔBKC cân tại B
Xét ΔBMK vuông tại M và ΔBAC vuông tại A có
BM=BA
\(\widehat{MBK}\) chung
Do đó: ΔBMK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B

Sửa đề: \(P=3x^7-4x^2+5x-9-3x^7-x-2\)
\(=\left(3x^7-3x^7\right)+\left(-4x^2\right)+\left(5x-x\right)+\left(-9-2\right)\)
\(=-4x^2+4x-11\)

a: ΔABC vuông tại C
=>\(\widehat{CBA}+\widehat{CAB}=90^0\)
=>\(\widehat{CAB}=90^0-35^0=55^0\)
Xét ΔCBA có \(\widehat{CBA}< \widehat{CAB}< \widehat{ACB}\)
mà CA,CB,AB lần lượt là cạnh đối diện của các góc CBA,CAB,ACB
nên CA<CB<AB
b: Xét ΔACM và ΔANM có
AC=AN
\(\widehat{CAM}=\widehat{NAM}\)
AM chung
Do đó: ΔACM=ΔANM
=>\(\widehat{ACM}=\widehat{ANM}\)
=>\(\widehat{ANM}=90^0\)
=>ΔANM vuông tại N
c: ΔACM=ΔANM
=>MC=MN
=>M nằm trên đường trung trực của CN(1)
Ta có: AN=AC
=>A nằm trên đường trung trực của CN(2)
Từ (1),(2) suy ra AM là đường trung trực của CN

Lời giải:
a.
$A=2x^2(x^2-2x+2)-x^4+x^3=2x^4-4x^3+4x^2-x^4+x^3$
$=(2x^4-x^4)+(-4x^3+x^3)+4x^2$
$=x^4-3x^3+4x^2$
$=1^4-3.1^3+4.1^2=1-3+4=2$
b.
$(2x-1)(x^2-x+1)=2x^3-3x^2+2$
$\Leftrightarrow 2x^3-3x^2+3x-1=2x^3-3x^2+2$
$\Leftrightarrow 3x-1=2$
$\Leftrightarrow 3x=3$
$\Leftrightarrow x=1$

Đa thức bậc 3 luôn có nghiệm bạn nhé. Đề sai bạn xem lại đề.

a: Xét ΔBAI vuông tại A và ΔBEI vuông tại E có
BI chung
BA=BE
Do đó: ΔBAI=ΔBEI
=>IA=IE
b: Xét ΔIAF vuông tại A và ΔIEC vuông tại E có
IA=IE
\(\widehat{AIF}=\widehat{EIC}\)(hai góc đối đỉnh)
Do đó: ΔIAF=ΔIEC
=>IF=IC
=>ΔIFC cân tại I
c: Xét ΔBFC có
CA,FE là các đường cao
CA cắt FE tại I
Do đó: I là trực tâm của ΔBFC
=>BI\(\perp\)FC
Ta có: ΔIAF=ΔIEC
=>AF=EC
Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//FC

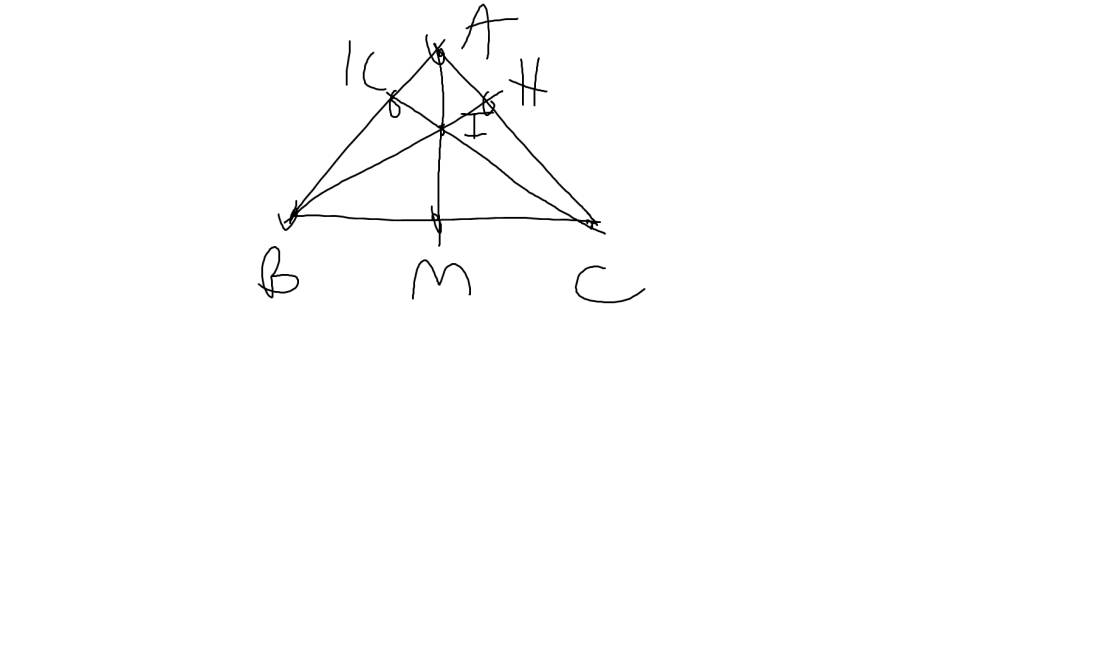
a: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-70^0}{2}=55^0\)
Xét ΔABC có \(\widehat{ACB}< \widehat{BAC}\)
mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC
nên AB<BC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>AH=AK
Xét ΔABC có \(\dfrac{AH}{AB}=\dfrac{AK}{AC}\)
nên HK//BC
d: Ta có: MH<MB(ΔMHB vuông tại H)
MK<MC(ΔMKC vuông tại K)
Do đó: MH+MK<MB+MC
=>MH+MK<2MC
mà HK<MH+MK
nên HK<2MC


\(\left(2x\right)^2\left(x-x^2\right)-4x\left(-x^3+x^2-5\right)=20\)
=>\(4x^2\left(x-x^2\right)-4x\left(-x^3+x^2-5\right)=20\)
=>\(4x^3-4x^4+4x^4-4x^3+20x=20\)
=>20x=20
=>x=1
F(x)=6x^3 -5x^2+7x-9,g(x)=2x^2-3x+5,h(x)=2x-1