cho tam giác DEF nhọn ( DE < DF ) , trên cạnh DE lấy điểm M sao cho DM = 2cm ; DE = 5cm ; trên cạnh DF lấy N sao cho DN = 6cm ; DF = 15cm . 1) chứng minh : DM/DE = DN/DF . 2) chứng minh : MN//EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó; ΔAHB~ΔBCD
b: Ta có: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>\(BD=15\left(cm\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(S_{ABD}=\dfrac{1}{2}\cdot AH\cdot BD=\dfrac{1}{2}\cdot AD\cdot AB\)
=>\(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=9\cdot12=108\)
=>AH=108/15=7,2(cm)
c: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(HB^2=12^2-7,2^2=9,6^2\)
=>HB=9,6(cm)
ΔHAB vuông tại H
=>\(S_{HAB}=\dfrac{1}{2}\cdot HA\cdot HB=\dfrac{1}{2}\cdot7,2\cdot9,6=34,56\left(cm^2\right)\)
Bài 1:
a: ΔACB vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=400=20^2\)
=>BC=20(cm)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{12}=\dfrac{DC}{16}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}\)
mà DB+DC=BC=20cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{20}{7}\)
=>\(DB=\dfrac{20}{7}\cdot3=\dfrac{60}{7}\left(cm\right);DC=4\cdot\dfrac{20}{7}=\dfrac{80}{7}\left(cm\right)\)
c: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔAHB~ΔCHA
d: Ta có: ΔABC~ΔHBA
=>\(\dfrac{AC}{HA}=\dfrac{BC}{BA}\)
=>\(\dfrac{16}{HA}=\dfrac{20}{12}=\dfrac{5}{3}\)
=>\(HA=16\cdot\dfrac{3}{5}=9,6\left(cm\right)\)


Ta có: \(5a^2+2b^2=11ab\)
\(\Leftrightarrow5a^2-11ab+2b^2=0\)
\(\Leftrightarrow5a^2-10ab-ab+2b^2=0\)
\(\Leftrightarrow5a\left(a-2b\right)-b\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(5a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-2b=0\\5a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=2b\\5a=b\end{matrix}\right.\) (1)
Lại có: \(a>\dfrac{b}{5}>0\Rightarrow5a>b\) (2)
Từ (1) và (2) \(\Rightarrow a=2b\)
Thay \(a=2b\) vào \(A\), ta được:
\(A=\dfrac{4\left(2b\right)^2-5b^2}{\left(2b\right)^2+3\cdot2b\cdot b}=\dfrac{16b^2-5b^2}{4b^2+6b^2}=\dfrac{11b^2}{10b^2}=\dfrac{11}{10}\)
Vậy \(A=\dfrac{11}{10}\) là giá trị cần tìm.

a: Xét ΔADB vuông tại D có DE là đường cao
nên \(AE\cdot AB=AD^2\left(1\right)\)
Xét ΔADC vuông tại D có DF là đường cao
nên \(AF\cdot AC=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
=>\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF~ΔACB
b: TH1: AD là đường trung tuyến
ΔABC vuông tại A có AD là đường trung tuyến
nên AD=DB=DC
\(\dfrac{1}{DB^2}+\dfrac{1}{DC^2}=\dfrac{1}{DA^2}+\dfrac{1}{DA^2}=\dfrac{2}{DA^2}\)
=>Đúng với GT

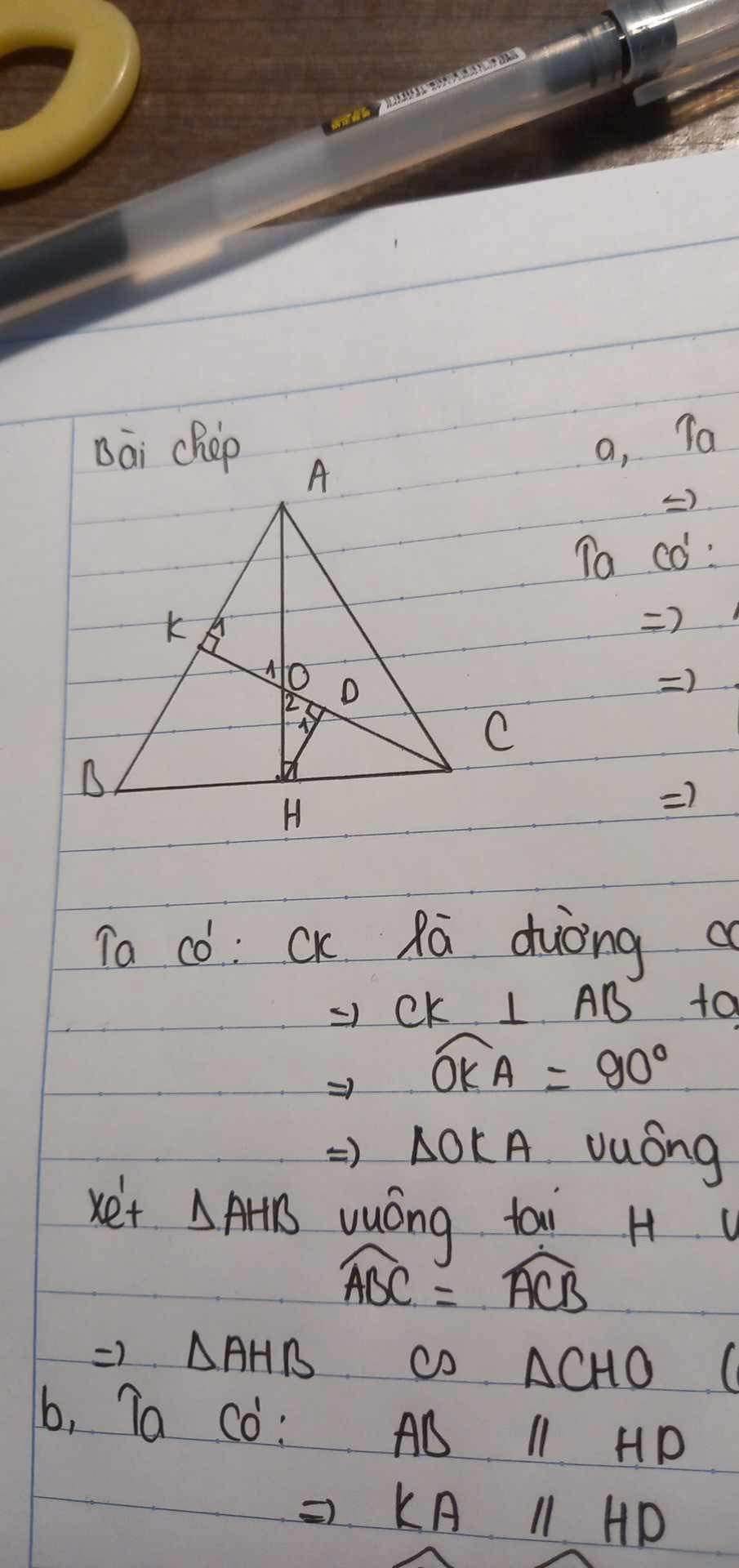
Đề bài cho tam giác ABC cân tại A đúng không em? Chỉ như vậy thì BK=2HD thôi
Ta có: H là trung điểm BC
\(BK||HD\) (cùng vuông góc CK)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{1}{2}BK\Rightarrow BK=2HD\)






1: \(\dfrac{DM}{DE}=\dfrac{2}{5}\)
\(\dfrac{DN}{DF}=\dfrac{6}{15}=\dfrac{2}{5}\)
Do đó: \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)
2: Xét ΔDEF có \(\dfrac{DM}{DE}=\dfrac{DN}{DF}\)
nên MN//EF