Giải phương trình:
a. (3x+5)3 + (2x-7)3 - (5x-2)3 = 0
b. (x2 + x - 2)3 + (x2 +5x +6)3 - 8(x2 + 3x +2)3 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
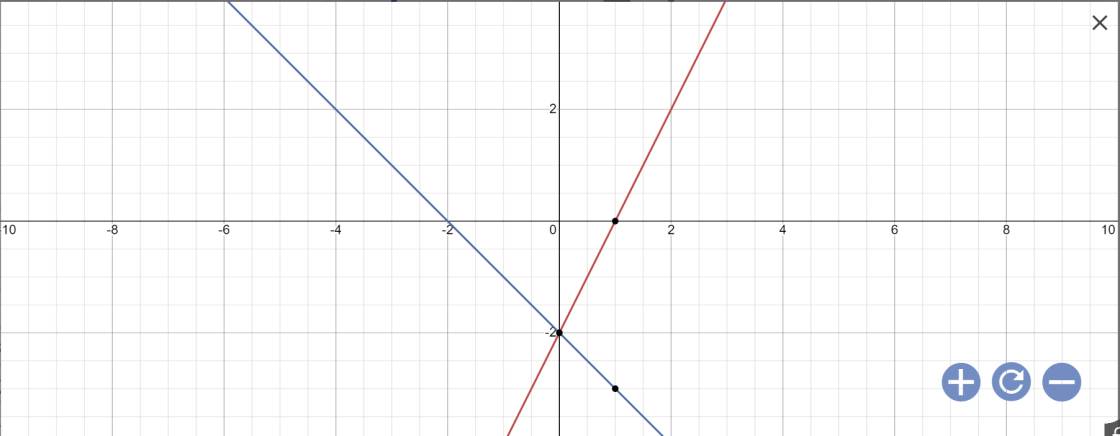
b: Tọa độ A là:
\(\left\{{}\begin{matrix}2x-2=-x-2\\y=2x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=0\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0-2=-2\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy: A(0;-2); B(1;0); C(-2;0)
\(AB=\sqrt{\left(1-0\right)^2+\left(0+2\right)^2}=\sqrt{5}\)
\(AC=\sqrt{\left(-2-0\right)^2+\left(0+2\right)^2}=2\sqrt{2}\)
\(BC=\sqrt{\left(-2-1\right)^2+\left(0-0\right)^2}=3\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{5+8-9}{2\cdot\sqrt{5}\cdot2\sqrt{2}}=\dfrac{4}{4\sqrt{10}}=\dfrac{1}{\sqrt{10}}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{1}{\sqrt{10}}\right)^2}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác BAC là:
\(S_{BAC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{5}\cdot2\sqrt{2}\cdot\dfrac{3}{\sqrt{10}}\)
\(=3\)

1: Xét ΔPMN có AB//MN
nên \(\dfrac{AB}{MN}=\dfrac{PA}{PM}\)
=>\(\dfrac{AB}{MN}=\dfrac{3}{7}\)
mà MN-AB=8
nên \(MN=8:\left(7-3\right)\cdot7=8:4\cdot7=14\left(cm\right)\)
=>AB=14-8=6(cm)
2:
a: Xét ΔABD có AE là phân giác
nên \(\dfrac{BE}{ED}=\dfrac{BA}{AD}\)
Xét ΔBAC có BF là phân giác
nên \(\dfrac{FA}{FC}=\dfrac{BA}{BC}=\dfrac{BA}{AD}\)
=>\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)
b:
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
\(\dfrac{BE}{ED}=\dfrac{FA}{FC}\)
=>\(\dfrac{BE}{ED}+1=\dfrac{FA}{FC}+1\)
=>\(\dfrac{BD}{ED}=\dfrac{AC}{FC}\)
mà BD=2OD và AC=2OC
nên \(\dfrac{2OD}{ED}=\dfrac{2OC}{FC}\)
=>\(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)
Xét ΔODC có \(\dfrac{OD}{ED}=\dfrac{OC}{FC}\)
nên EF//CD

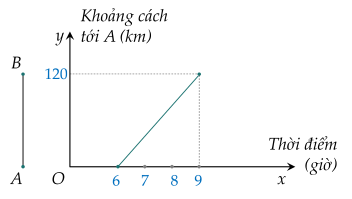
a: Đặt (d): y=ax+b
Theo đồ thị, ta sẽ thấy: (d) đi qua A(6;0) và B(9;120)
Thay x=6 và y=0 vào y=ax+b, ta được:
\(a\cdot6+b=0\)
=>6a+b=0(1)
Thay x=9 và y=120 vào y=ax+b, ta được:
\(a\cdot9+b=120\)
=>9a+b=120(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}9a+b=120\\6a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9a+b-6a-b=120\\6a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=120\\b=-6a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=40\\b=-240\end{matrix}\right.\)
b: a=40; b=-240
=>y=40x-240
Thay x=8 vào y=40x-240, ta được:
\(y=40\cdot8-240=80\left(km\right)\)
=>Ô tô còn cách B 120-80=40km

a: Vì đường thẳng y=ax+b song song với đường thẳng y=3x-7 nên \(\left\{{}\begin{matrix}a=3\\b\ne-7\end{matrix}\right.\)
=>y=3x+b
Thay x=1 và y=2 vào y=3x+b, ta được:
\(b+3\cdot1=2\)
=>b+3=2
=>b=-1
Vậy: y=3x-1
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-7=-3x+3\\y=2x-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=10\\y=2x-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\cdot2-7=-3\end{matrix}\right.\)
Thay x=2 và y=-3 vào y=ax+b, ta được:
\(a\cdot2+b=-3\)
=>2a+b=-3(1)
Thay x=-2 và y=5 vào y=ax+b, ta được:
\(a\cdot\left(-2\right)+b=5\)
=>-2a+b=5(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=-3\\-2a+b=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-2a+b=-3+5\\2a+b=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=2\\2a=-3-b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\2a=-3-1=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)

a:
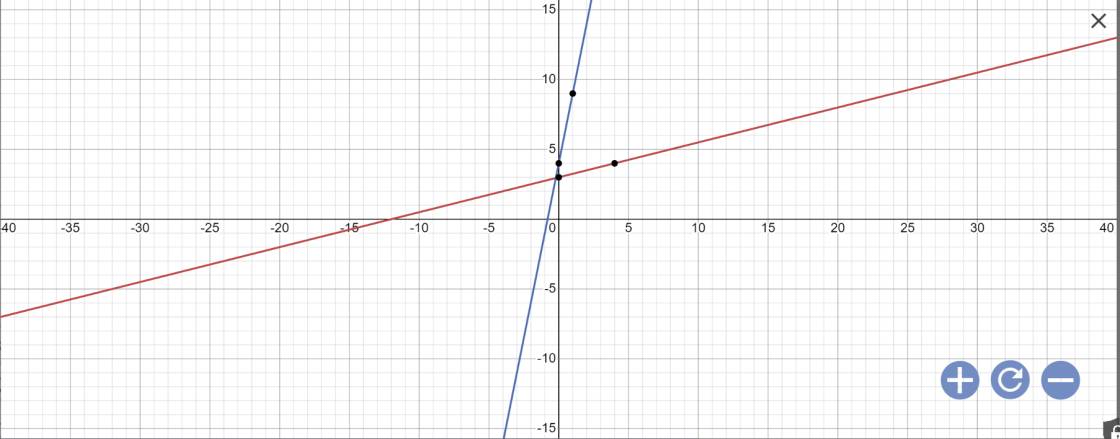
b: Tọa độ giao điểm của d1 với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{4}x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{x}{4}=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-12\\y=0\end{matrix}\right.\)
Vậy: (d1) giao Ox tại A(-12;0)
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{4}x+3=\dfrac{1}{4}\cdot0+3=3\end{matrix}\right.\)
vậy: (d1) giao Oy tại B(0;3)

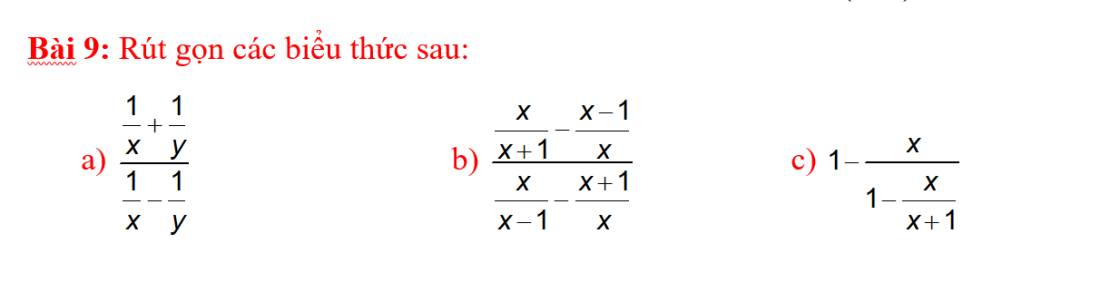
a:
ĐKXĐ: \(x\ne0;y\ne0\)
\(\dfrac{\dfrac{1}{x}+\dfrac{1}{y}}{\dfrac{1}{x}-\dfrac{1}{y}}=\dfrac{x+y}{xy}:\dfrac{x-y}{xy}=\dfrac{x+y}{xy}\cdot\dfrac{xy}{x-y}=\dfrac{x+y}{x-y}\)
b:
ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)
\(\dfrac{\dfrac{x}{x+1}-\dfrac{x-1}{x}}{\dfrac{x}{x-1}-\dfrac{x+1}{x}}\)
\(=\left(\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}\right):\dfrac{x^2-\left(x-1\right)\left(x+1\right)}{x\left(x-1\right)}\)
\(=\dfrac{x^2-x^2+1}{x\cdot\left(x+1\right)}\cdot\dfrac{x\left(x-1\right)}{x^2-x^2+1}\)
\(=\dfrac{x-1}{x+1}\)
c:
ĐKXĐ: \(x\ne-1\)
\(1-\dfrac{x}{1-\dfrac{x}{x+1}}\)
\(=1-\dfrac{x}{\dfrac{x+1-x}{x+1}}\)
\(=1-\dfrac{x}{\dfrac{1}{x+1}}\)
\(=1-x\left(x+1\right)=1-x^2-x\)



a) \(\left(3x+5\right)^3+\left(2x-7\right)^3-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left[\left(3x+5\right)+\left(2x-7\right)\right]\left[\left(3x+5\right)^2-\left(3x+5\right)\left(2x-7\right)+\left(2x-7\right)^2\right]-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left[9x^2+30x+25-\left(6x^2-21x+10x-35\right)+4x^2-28x+49\right]-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left(7x^2+13x+109\right)-\left(5x-2\right)^3=0\)
\(\Leftrightarrow\left(5x-2\right)\left[7x^2+13x+109-\left(5x-2\right)^2\right]=0\)
\(\Leftrightarrow\left(5x-2\right)\left(7x^2+13x+109-25x^2+20x-4\right)=0\)
\(\Leftrightarrow\left(5x-2\right)\left(-18x^2+33x+105\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(6x^2-11x-35\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(6x^2+10x-21x-35\right)=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left[2x\left(3x+5\right)-7\left(3x+5\right)\right]=0\)
\(\Leftrightarrow-3\left(5x-2\right)\left(2x-7\right)\left(3x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-2=0\\2x-7=0\\3x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{5}\\x=\dfrac{7}{2}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
a: Đặt \(3x+5=a;2x-7=b\)
=>a+b=3x+5+2x-7=5x-2
Phương trình ban đầu sẽ trở thành:
\(a^3+b^3-\left(a+b\right)^3=0\)
=>\(\left(a+b\right)^3-3ab\left(a+b\right)-\left(a+b\right)^3=0\)
=>-3ab(a+b)=0
=>ab(a+b)=0
=>(3x+5)(2x-7)(5x-2)=0
=>\(\left[{}\begin{matrix}3x+5=0\\2x-7=0\\5x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\\x=\dfrac{7}{2}\\x=\dfrac{2}{5}\end{matrix}\right.\)
b: \(\left(x^2+x-2\right)^3+\left(x^2+5x+6\right)^3-8\left(x^2+3x+2\right)^3=0\)
=>\(\left(x^2+x-2\right)^3+\left(x^2+5x+6\right)^3-\left(2x^2+6x+4\right)^3=0\)(2)
Đặt \(x^2+x-2=c;x^2+5x+6=d\)
=>\(c+d=2x^2+6x+4\)
Phương trình (2) sẽ trở thành:
\(c^3+d^3-\left(c+d\right)^3=0\)
=>\(\left(c+d\right)^3-3cd\left(c+d\right)-\left(c+d\right)^3=0\)
=>-3cd(c+d)=0
=>cd(c+d)=0
=>\(\left(x^2+x-2\right)\left(x^2+5x+6\right)\left(2x^2+6x+4\right)=0\)
=>\(\left(x+2\right)\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+2\right)\left(x+1\right)=0\)
=>\(\left(x+2\right)^3\cdot\left(x-1\right)\left(x+1\right)\left(x+3\right)=0\)
=>\(\left[{}\begin{matrix}x=-2\\x=1\\x=-1\\x=-3\end{matrix}\right.\)