chứng minh rằng , nếu a\(\ge\)0 và b\(\ge\)0 thì \(\frac{a+b}{2}\times\frac{a^2+b^2}{2}\le\frac{a^3+b^3}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\left[\frac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\frac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]\cdot\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\frac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}=\frac{x-1}{x}\)
Để P > 1/2 thì \(\frac{x-1}{x}>\frac{1}{2}\Leftrightarrow\frac{x-1}{x}-\frac{1}{2}>0\Leftrightarrow\frac{2x-2-x}{2x}>0\Leftrightarrow\frac{x-2}{2x}>0\)(1)
Vì x > 0 nên 2x > 0 nên (1) <=> x - 2 > 0 <=> x > 2


giá trị nhỏ nhất của hàm số y= 2x^2 - 4
= 2x^2 - 4
= -4
nha bạn


A B C H O K L N M E F G
Trên EF lấy điểm G sao cho \(HG\perp OA\) (Định nghĩa lại điểm G)
Ta thấy đường tròn (HAC) và (O) đối xứng nhau qua AC, suy ra AOCK là hình thoi
Từ đó \(\widehat{OAM}=180^0-\widehat{AMK}=\widehat{AHK}=90^0-\widehat{ACH}=\widehat{BAC}\)
Suy ra \(\widehat{CAM}=\widehat{BAO}=\widehat{CAH}\) hay AC là phân giác của \(\widehat{HAM}\)
Vì MK là phân giác ngoài của \(\widehat{AMH}\) do K là điểm chính giữa cung AMH nên C là tâm bàng tiếp góc A của \(\Delta AHM\)
Do đó \(\frac{CE}{CA}=\frac{HE}{HA}\). Hoàn toàn tương tự \(\frac{BA}{BF}=\frac{HA}{HF}\)
Mặt khác AMHN là hình bình hành do (AKH),(ALH) đối xứng nhau qua trung điểm AH, đồng thời
\(\widehat{MAN}=\widehat{MHN}=\widehat{AHM}+\widehat{AHN}=180^0-\widehat{AOB}+180^0-\widehat{AOC}=2\widehat{BAC}=2\widehat{OAM}\)
Suy ra AO là phân giác của \(\widehat{MAN}\), mà \(HG\perp AO\) nên HG là phân giác ngoài của \(\widehat{MHN}\)
Do vậy \(\frac{GF}{GE}=\frac{HF}{HE}\). Vậy ta có \(\frac{CE}{CA}.\frac{BA}{BF}.\frac{GF}{GE}=1\), suy ra G,B,C thẳng hàng.


vì \(2^n-1\) là số nguyên tố nên tổng các ước của \(2^n-1\) là \(1+2^n-1\)
tổng các ước của \(2^{n-1}\left(2^n-1\right)\) là \(\displaystyle\Sigma ^{n-1}_{i=0}(2^i)\times (1+2^n-1)\)\(=\left(2^n-1\right)\times2^n=2\left[2^{n-1}\left(2^n-1\right)\right]\)
Vậy số đã cho là số hoàn hảo
 nha bạn
nha bạn 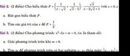

 g
g