Trong một bảng ô vuông gồm có 5 x 5 vuông, người ta viết vào mỗi ô vuông chỉ một trong 3 số 1; 0; -1. Chứng minh rằng trong các tổng của 5 số theo mỗi cột, mỗi hàng, mỗi đường chéo phải có ít nhất hai tổng số bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AH
Akai Haruma
Giáo viên
6 tháng 5 2024
Lời giải:
$\frac{2x+1}{-27}=\frac{-3}{2x+1}$
$\Rightarrow (2x+1)^2=(-27)(-3)$
$\Rightarrow (2x+1)^2=81=9^2=(-9)^2$
$\Rightarrow 2x+1=9$ hoặc $2x+1=-9$
$\Rightarrow x=4$ hoặc $x=-5$
KV
5 tháng 5 2024
Do P(x) chia hết cho x - 1 nên nghiệm của đa thức x - 1 cũng là nghiệm của P(x)
Cho x - 1 = 0
x = 0 + 1
x = 1
⇒ P(1) = a.1² + b.1 + c
= a + b + c
= 0
Vậy S = 0
5 tháng 5 2024
a: Kẻ DM//AC(M\(\in\)AC)
Ta có: DM//AC
=>\(\widehat{BMD}=\widehat{BCA}\)(hai góc đồng vị)
=>\(\widehat{DBM}=\widehat{DMB}\)
=>DB=DM
=>DM=CE
Xét ΔDIM và ΔEIC có
\(\widehat{DMI}=\widehat{ECI}\)(DM//CE)
DM=CE
\(\widehat{MDI}=\widehat{CEI}\)(DM//CE)
Do đó: ΔDIM=ΔEIC
=>ID=IE
=>I là trung điểm của DE
b: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
Xét ΔABO và ΔACO có
AB=AC
\(\widehat{BAO}=\widehat{CAO}\)
AO chung
Do đó: ΔABO=ΔACO
=>\(\widehat{ABO}=\widehat{ACO}=90^0\)
=>OC\(\perp\)AE tại C
Ta có: ΔABO=ΔACO
=>OB=OC
Xét ΔOBD vuông tại B và ΔOCE vuông tại C có
OB=OC
BD=CE
Do đó: ΔOBD=ΔOCE
=>OD=OE
=>ΔODE cân tại O
Ta có: ΔODE cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)DE
5 tháng 5 2024
a: Xét ΔBAH vuông tại A và ΔBMH vuông tại M có
BH chung
\(\widehat{ABH}=\widehat{MBH}\)
Do đó: ΔBAH=ΔBMH
b: ΔBAH=ΔBMH
=>BA=BM và HA=HM
Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
ta có: HA=HM
=>H nằm trên đường trung trực của AM(2)
Từ (1),(2) suy ra BH là đường trung trực của AM
c: Xét ΔBMN vuông tại M và ΔBAC vuông tại A có
BM=BA
\(\widehat{MBN}\) chung
Do đó: ΔBMN=ΔBAC
=>BN=BC
Xét ΔBNC có \(\dfrac{BA}{BN}=\dfrac{BM}{BC}\)
nên AM//NC
d: Xét ΔBNC có
NM,CA là các đường cao
NM cắt CA tại H
Do đó: H là trực tâm của ΔBNC
=>BH\(\perp\)CN
LT
1
5 tháng 5 2024
Bài 3:
a: \(f\left(x\right)=3x^2-7+5x-6x^2+4x^3+8+5x^5+x^3\)
\(=5x^5+\left(4x^3+x^3\right)+\left(3x^2-6x^2\right)+5x+\left(-7+8\right)\)
\(=5x^5+5x^3-3x^2+5x+1\)
\(g\left(x\right)=x^2-7x+5x-7x^2+2x^3+7x+10x^5-x^3+2\)
\(=10x^5+\left(-x^3+2x^3\right)+\left(x^2-7x^2\right)+\left(-7x+5x+7x\right)+2\)
\(=10x^5+x^3-5x^2+5x+2\)
b: h(x)=f(x)+g(x)
\(=5x^5+5x^3-3x^2+5x+1+10x^5+x^3-5x^2+5x+2\)
\(=15x^5+6x^3-8x^2+10x+3\)
k(x)=2f(x)-g(x)
\(=2\left(5x^5+5x^3-3x^2+5x+1\right)-\left(10x^5+x^3-5x^2+5x+2\right)\)
\(=10x^5+10x^3-6x^2+10x+2-10x^5-x^3+5x^2-5x-2\)
\(=9x^3-x^2+5x\)
c: \(h\left(1\right)=15\cdot1^5+6\cdot1^3-8\cdot1^2+10\cdot1+3\)
=15+6-8+10+3
=13+13
=26
d: Đặt K(x)=0
=>\(9x^3-x^2+5x=0\)
=>\(x\left(9x^2-x+5\right)=0\)
mà \(9x^2-x+5>0\forall x\)
nên x=0
Câu 1:
a: Xét ΔAHB và ΔAHC có
AB=AC
BH=CH
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
=>AH\(\perp\)BC
b: Xét ΔIBC có
IH là đường cao
IH là đường trung tuyến
Do đó: ΔIBC cân tại I
TM
2
5 tháng 5 2024
\(2x^3-4x^2+3x+a-10⋮x-2\)
=>\(2x^3-4x^2+3x-6+a-4⋮x-2\)
=>a-4=0
=>a=4
KV
6 tháng 5 2024
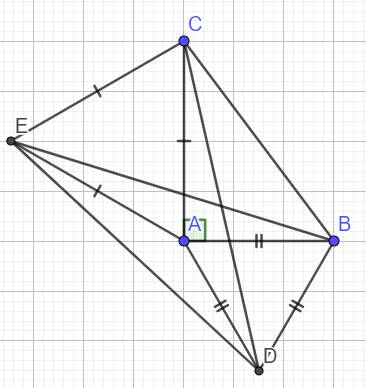
a) \(\Delta ABD\) đều (gt)
\(\Rightarrow\widehat{DAB}=60^0\)
\(\Rightarrow\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=60^0+90^0=150^0\)
\(\Delta ACE\) đều (gt)
\(\Rightarrow CAE=60^0\)
\(\Rightarrow\widehat{EAB}=\widehat{CAE}+\widehat{BAC}=60^0+90^0=150^0\)
\(\Rightarrow\widehat{EAB}=\widehat{DAC}=150^0\)
Xét \(\Delta ABE\) và \(\Delta ADC\) có:
\(AB=AD\) (do \(\Delta ABD\) đều)
\(\widehat{EAB}=\widehat{DAC}\left(cmt\right)\)
\(AE=AC\) (do \(\Delta ACE\) đều)
\(\Rightarrow\Delta ABE=\Delta ADC\left(c-g-c\right)\)
b) Gọi \(F\) là giao điểm của \(CA\) và \(DE\)
Ta có:
\(\widehat{FAD}=\widehat{FAB}-\widehat{DAB}=\widehat{CAB}-\widehat{DAB}=90^0-60^0=30^0\)
\(\widehat{EAF}+\widehat{CAE}=180^0\) (kề bù)
\(\Rightarrow\widehat{EAF}=180^0-\widehat{CAE}=180^0-60^0=120^0\)
\(\Rightarrow\widehat{EAD}=\widehat{EAF}+\widehat{FAD}=120^0+30^0=150^0\)
\(\Rightarrow\widehat{EAD}=\widehat{EAB}=150^0\)
Xét \(\Delta ADE\) và \(\Delta ABE\) có:
\(AD=AB\left(cmt\right)\)
\(\widehat{EAD}=\widehat{EAB}\left(cmt\right)\)
\(AE\) là cạnh chung
\(\Rightarrow\Delta ADE=\Delta ABE\left(c-g-c\right)\)
\(\Rightarrow DE=BE\) (hai cạnh tương ứng)