Hàm số bậc nhất có dạng: \(y=ax+b\left(a\ne0\right)\)

Có: \(y=-\left(5x-8+9x\right)+3=-5x+8-9x+3=-14x+11\)

=> Là hàm số bậc nhất.

Cho đường thẳng (d): (y=(2m+1)x-2) với m là tham số và (m\ne-\frac{1}{2}.) Khoảng cách từ (A(-2;1)) đến đường thẳng d được tính theo công thức:

[\sqrt{(-2-(2m+1)(-2))^2+(1-(2m+1)(-2))^2}]

[\sqrt{(16m^2+20m+4)^2+(24m+4)^2}]

[\sqrt{256m^4+640m^3+320m^2+576m^2+960m+16}]

[\sqrt{256m^4+1216m^3+1536m^2+960m+16}]

[\sqrt{16m^2(16m^2+79m+96)+4(16m^2+79m+96)}]

[\sqrt{(4m+7)^2(4m+16)}]

Theo đề bài, khoảng cách này bằng (\frac{1}{\sqrt{2}}.) Do đó, ta có phương trình:

[\sqrt{(4m+7)^2(4m+16)}=\frac{1}{\sqrt{2}}]

Từ đây, ta được phương trình bậc hai:

[(4m+7)^2(4m+16)=1 ]

Giải phương trình này, ta được hai nghiệm:

[m=-\frac{3}{2}\pm\frac{\sqrt{3}}{2} ]

Do (m\ne-\frac{1}{2},) ta có nghiệm duy nhất là:

[m=-\frac{3}{2}+\frac{\sqrt{3}}{2}=\frac{5}{7} ]

Vậy, tổng các giá trị của m thỏa mãn bài toán là [\frac{5}{7}.]

Tổng 2 vận tốc:

210:2=105(km/h)

Vận tốc xe máy:

(105 - 15):2= 45(km/h)

Đ.số: xe máy có vận tốc 45km/h

Lời giải:
PT hoành độ giao điểm:

$(m^2+1)x-12m+5=x+5$
$\Leftrightarrow m^2x-12m=0(*)$
Để 2 đths cắt nhau tại 1 điểm có hoành độ $x=2$ thì $x=2$ phải là nghiệm của $(*)$

$\Rightarrow m^2.2-12m=0$

$\Leftrightarrow 2m(m-6)=0$

$\Rightarrow m=0$ hoặc $m=6$

nui

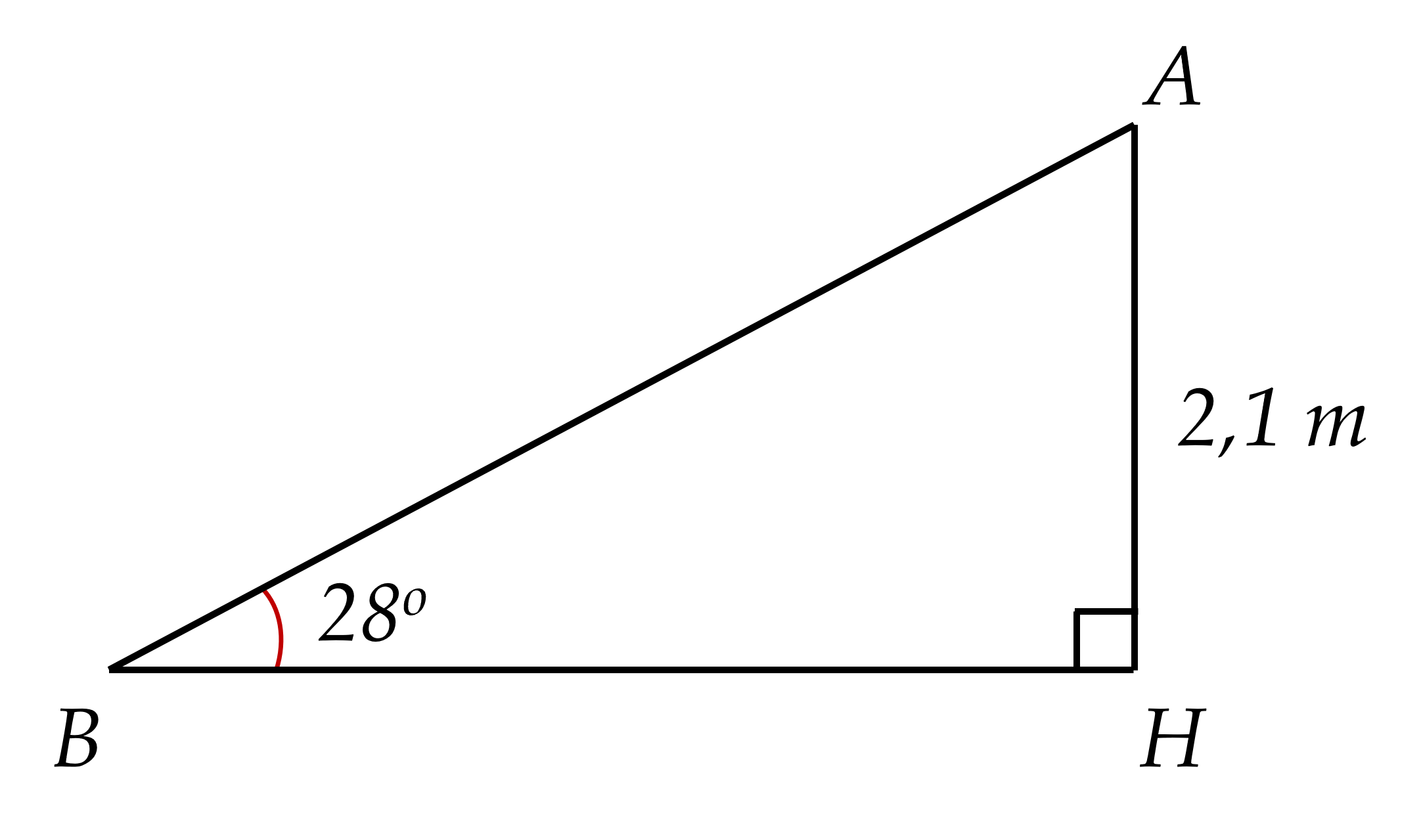
1) Xét △ABH vuông tại H có:

      \(\sin\widehat{ABH}=\dfrac{AH}{AB}\)(tỉ số lượng giác)

 ⇒ \(AB=\dfrac{AH}{\sin\widehat{ABH}}=\dfrac{2,1}{\sin28^o}\approx4,5\left(m\right)\)

Vậy độ dài của mặt cầu trượt khoảng 4,5m.

2) 

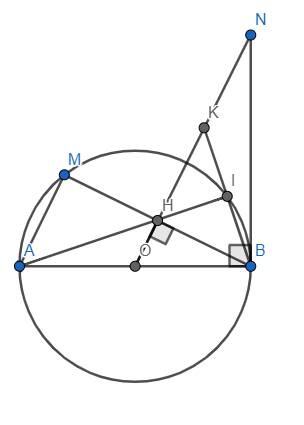
a) Xét △AMB có: A, M, B ∈ (O) (gt)

                              AB là đường kính của (O) (gt)

  ⇒ △AMB vuông tại M(ĐL về sự xác định của đường tròn)

   Xét △AMB vuông tại M có: O là trung điểm AB(gt)

                                                  OH // AM (⊥ MB)

  ⇒ OH là đường trung bình của △AMB

  ⇒ H là trung điểm của MB (t/c)(đpcm)

  Xét △NMB có: H là trung điểm của MB(cmt)

                         NH ⊥ MB(do N ∈ OH ⊥ MB)

  ⇒ NH là đường trung tuyến đồng thời cũng là đường cao trong △NMB

  ⇒ △NMB cân tại N(t/c △ cân)

  ⇒ NM = NB(t/c △ cân)

  Xét △NMO và △NBO có:

      ON chung

      NM = NB(cmt)

      OM = OB(= R)

  ⇒ △NMO = △NBO (c.c.c)

  ⇒ \(\widehat{NMO}=\widehat{NBO}=90^o\)

  ⇒ NM ⊥ MO

  Mà OM = R

  ⇒ MN là tiếp tuyến của đường tròn (O; R) (đpcm)

b) Xét △MAB và △HBN có: 

     \(\widehat{AMB}=\widehat{BHN}=90^o\)

     \(\widehat{MBA}=\widehat{HNB}\) (do cùng phụ với \(\widehat{NOB}\))

 ⇒ △MAB ∼ △HBN (g.g)(đpcm)