Cho hai đa thức P(x) = 4\(^{ }\)\(^{ }\)x^3 - 3x^2 +7 và Q(x)= -2x^3 + 5x^2 -2x +3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai lần hiệu của a và b là:
\(2\left(a-b\right)=2a-2b\)

Câu 6:
a: Đặt M(x)=0
=>\(2x-\dfrac{1}{2}=0\)
=>\(2x=\dfrac{1}{2}\)
=>\(x=\dfrac{1}{4}\)
b: Đặt N(x)=0
=>\(\left(x+5\right)\left(4x^2-1\right)=0\)
=>(x+5)(2x-1)(2x+1)=0
=>\(\left[{}\begin{matrix}x+5=0\\2x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
c: Đặt P(x)=0
=>\(9x^3-25x=0\)
=>\(x\cdot\left(9x^2-25\right)=0\)
=>x(3x-5)(3x+5)=0
=>\(\left[{}\begin{matrix}x=0\\3x-5=0\\3x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
Câu 7:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
b: Xét ΔBDE và ΔBHA có
BD=BH
\(\widehat{DBE}=\widehat{HBA}\)(hai góc đối đỉnh)
BE=BA
Do đó: ΔBDE=ΔBHA
=>\(\widehat{BDE}=\widehat{BHA}\)
=>AH//DE
c: Ta có: AH=DE
mà AH<AD(ΔAHD vuông tại H)
nên DE<DA
Xét ΔDAE có DE<DA
mà \(\widehat{DAE};\widehat{DEA}\) lần lượt là góc đối diện của các cạnh DE,DA
nên \(\widehat{DAE}< \widehat{DEA}\)
=>\(\widehat{DAB}< \widehat{BAH}\)

a: Cô An hơn Tuấn:
2014-1986=28(tuổi)
b: Gọi số năm nữa để tuổi cô An gấp 5 lần tuổi Tuấn là x(năm)
(Điều kiện: x>0)
Tuổi của cô An vào năm 2014 là 28(tuổi)
Tuổi của cô An sau x năm nữa là x+28(tuổi)
Tuổi của Tuấn sau x năm nữa là x(tuổi)
Theo đề, ta có:
5x=x+28
=>4x=28
=>x=7
Năm mà tuổi cô An gấp 5 lần tuổi tuấn là:
2014+7=2021
Khi đó, Tuấn 7 tuổi

Bài 3:
a: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có
CA chung
AB=AE
Do đó: ΔCAB=ΔCAE
b: Xét ΔCEB có
CA,BH là các đường trung tuyến
CA cắt BH tại M
Do đó: M là trọng tâm của ΔCEB
=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot18=12\left(cm\right)\)
c: Xét ΔCEB có
A là trung điểm của BE
AK//CE
Do đó: K là trung điểm của CB
Xét ΔCEB có
M là trọng tâm
K là trung điểm của CB
Do đó: E,M,K thẳng hàng

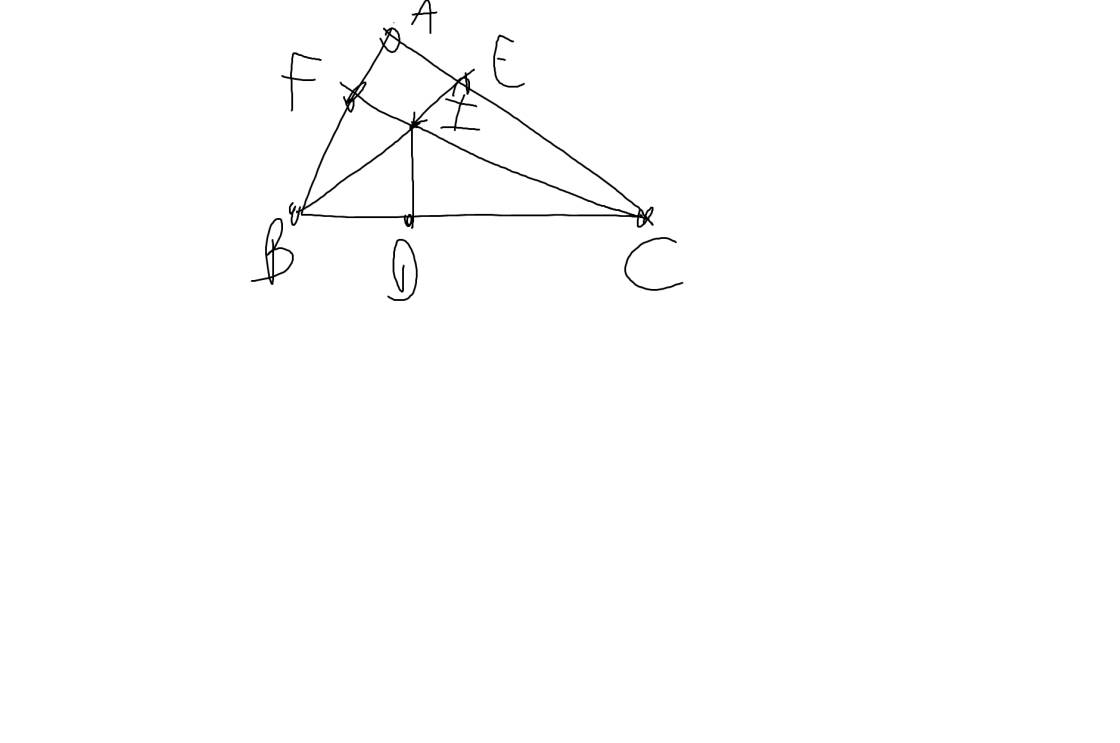
a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ABC}+50^0+70^0=180^0\)
=>\(\widehat{ABC}=60^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia BC, ta có: \(\widehat{CBI}< \widehat{CBA}\left(30^0< 60^0\right)\)
nên tia BI nằm giữa hai tia BC và BA
Ta có: tia BI nằm giữa hai tia BC và BA
mà \(\widehat{CBI}=\dfrac{1}{2}\cdot\widehat{CBA}\)
nên BI là phân giác của góc ABC
Trên cùng một nửa mặt phẳng bờ chứa tia CB, ta có: \(\widehat{BCI}< \widehat{BCA}\)
nên tia CI nằm giữa hai tia CB và CA
Ta có: tia CI nằm giữa hai tia CB và CA
mà \(\widehat{BCI}=\dfrac{1}{2}\cdot\widehat{BCA}\)
nên CI là phân giác của góc BCA
c: Xét ΔBFI vuông tại F và ΔBDI vuông tại D có
BI chung
\(\widehat{FBI}=\widehat{DBI}\)
Do đó: ΔBFI=ΔBDI
=>IF=ID
Xét ΔCDI vuông tại D và ΔCEI vuông tại E có
CI chung
\(\widehat{DCI}=\widehat{ECI}\)
Do đó: ΔCDI=ΔCEI
=>ID=IE
=>ID=IE=IF
=>I là giao điểm của 3 đường trung trực của ΔDEF

a: Sửa đề: Chứng minh ΔNMQ=ΔNHQ
Xét ΔNMQ vuông tại M và ΔNHQ vuông tại H có
NQ chung
\(\widehat{MNQ}=\widehat{HNQ}\)
Do đó: ΔNMQ=ΔNHQ
b: Q thuộc MP
=>Q nằm giữa M và P
=>QM+QP=PM
=>MP>PQ

a: Xét ΔBAI và ΔBDI có
BA=BD
AI=DI
BI chung
Do đó: ΔBAI=ΔBDI
b: ΔBAI=ΔBDI
=>\(\widehat{ABI}=\widehat{DBI}\)
Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}\)
=>\(\widehat{BDE}=90^0\)
=>ED\(\perp\)BC
Gọi M là giao điểm của CK với BA
Xét ΔBMC có
BK,CA là các đường cao
BK cắt CA tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
=>M,E,D thẳng hàng
=>BA,ED,CK đồng quy


Đề yêu cầu gì em nhỉ?