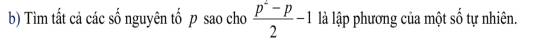Cho \(\Delta ABC\) nhọn nội tiếp đường tròn \(\left(O\right)\). Đường cao \(AD,BE,CF\) cắt nhau tại \(H\). Gọi \(M\) là trung điểm của \(BC\). Từ \(A\) kẻ đường thẳng cắt \(BC\) tại \(K\) (\(K\) nằm ngoài đường tròn). \(HM\) cắt \(AK\) tại \(G\). Chứng minh rằng:
\(a\)) Tứ giác \(BFEC\) nội tiếp đường tròn.
\(b\)) \(HG\perp AK\).
\(c\)) Tứ giác \(BHCN\) là hình bình hành.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

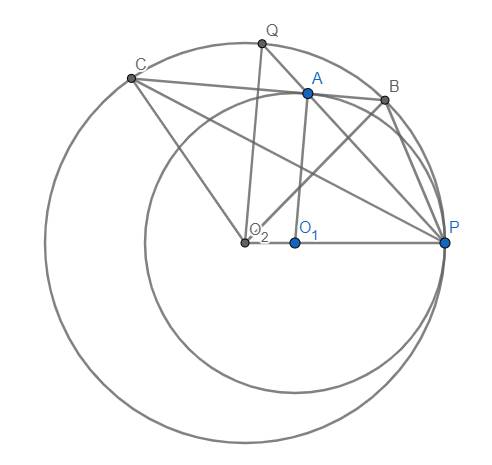
Gọi Q là giao điểm của PA và (O2). Do \(\widehat{O_1AP}=\widehat{O_1PA}=\widehat{O_2PQ}=\widehat{O_2QP}\) nên O1A//O2Q
Mặt khác, \(BC\perp O_1A\) (vì BC là tiếp tuyến tại A của (O1) nên \(BC\perp O_2Q\)
\(\Rightarrow\) Q là điểm chính giữa của cung nhỏ BC
\(\Rightarrow\) PQ là tia phân giác \(\widehat{BPC}\) \(\Rightarrow\) đpcm

Nếu như theo kiến thức lớp 9 chưa học về đồ thị nào khác ngoài đồ thị bậc nhất (là 1 đường thẳng) thì 2 dạng bài này gần như tương đương nhau. Nhưng khi bạn lên cấp III và học những loại đồ thị đường cong bậc hai (ellipse, parabol, hyperbol, đường tròn,...) thì 2 dạng bài này rõ ràng khác xa nhau nhé. (Vì xác định hàm số thì đó có thể là hàm số kiểu gì cũng được, nhưng viết ptđt thì chỉ có liên quan đến đường thẳng thôi.)

Lời giải:
a.
\(M=\frac{x}{\sqrt{x}(\sqrt{x}-1)}-\frac{2\sqrt{x}-1}{\sqrt{x}(\sqrt{x}-1)}=\frac{x-(2\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}\\ =\frac{x-2\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)}=\frac{(\sqrt{x}-1)^2}{\sqrt{x}(\sqrt{x}-1)}\\ =\frac{\sqrt{x}-1}{\sqrt{x}}\)
b.
$M=-2\Leftrightarrow \frac{\sqrt{x}-1}{\sqrt{x}}=-2$
$\Leftrightarrow \sqrt{x}-1=-2\sqrt{x}$
$\Leftrightarrow 3\sqrt{x}=1\Leftrightarrow x=\frac{1}{9}$ (tm)


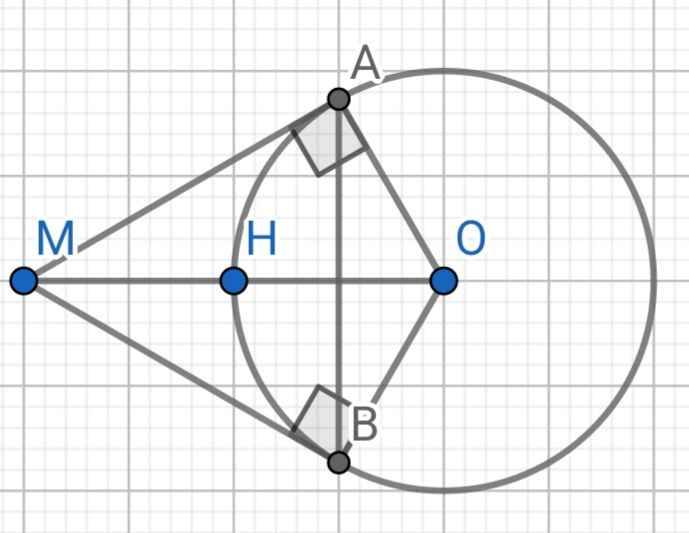 a)
a)
Ta có:
OH = R = 12 (cm)
OM = 2R (gt)
⇒ OM = 2.12 = 24 (cm)
∆OAM vuông tại A
⇒ OM² = OA² + AM² (Pytago)
⇒ AM² = OM² - OA²
= 24² - 12²
= 432
⇒ AM = 12√3 (cm)
b) ∆OAM vuông tại A
⇒ sin AMO = OA/OM = 1/2
⇒ ∠AMO = 30⁰
Do MA và MB là hai tiếp tuyến cắt nhau tại M
⇒ MO là tia phân giác của ∠AMB
⇒ ∠BMO = ∠AMO = 30⁰
⇒ ∠AMB = ∠AMO + ∠BMO
= 30⁰ + 30⁰
= 60⁰
Do MA và MB là hai tiếp tuyến cắt nhau tại M
⇒ MA = MB
⇒ ∆ABM cân tại M
Mà ∠AMB = 60⁰ (cmt)
⇒ ∆ABM là tam giác đều

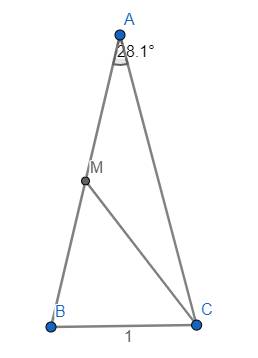
Không mất tổng quát, giả sử \(BC=1\).
Từ gt \(\Rightarrow\widehat{BAC}=180^o-2\widehat{ABC}=28^o5'22''\)
Áp dụng định lý sin cho tam giác ABC, ta có:
\(\dfrac{AC}{\sin B}=\dfrac{BC}{\sin A}\Rightarrow AC=\dfrac{BC\sin B}{\sin A}\) \(=\dfrac{\sin\left(75^o57'19''\right)}{\sin\left(28^o5'22''\right)}=2k\)
Mà tam giác ABC cân tại A nên \(AB=AC=2k\)
\(\Rightarrow MB=MA=k\)
Có \(MC=\sqrt{\dfrac{2\left(CA^2+CB^2\right)-AB^2}{4}}\) \(=\sqrt{\dfrac{2\left(4k^2+1\right)-4k^2}{4}}\) \(=\dfrac{\sqrt{4k^2+2}}{2}\) (Công thức tính độ dài đường trung tuyến trong tam giác, mình không chứng minh ở đây nhé.)
Áp dụng định lý sin cho tam giác ACM, có:
\(\dfrac{AM}{\sin\widehat{ACM}}=\dfrac{CM}{\sin\widehat{A}}\) \(\Rightarrow\sin\widehat{ACM}=\dfrac{AM\sin A}{CM}\) \(=\dfrac{k\sin\left(28^o5'22''\right)}{\dfrac{\sqrt{4k^2+2}}{2}}\)
\(\Rightarrow...\)