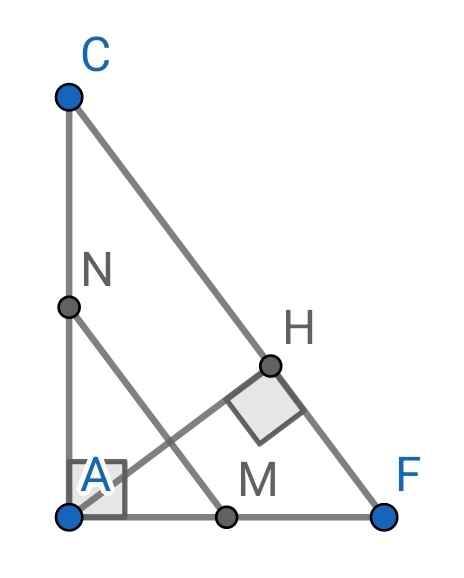
cho tam giác abc vuông tại a, ah đường cao a, cmr tam giác abc đồng dạng tam giác hba.
b, cmr AH^2=Hb.HC
c. vẽ trung tuyết AM, từ H vẽ HD vuông góc AB tại D, vẽ HE vuông góc AC tại E, cmr Am vuông góc DE
mình nhờ các bạn giải giúp câu c ạ, mình cảm ơn




a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: XétΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HB\cdot HC=HA^2\)
c: Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>\(\widehat{MAC}=\widehat{ACB}\)
\(\widehat{MAC}+\widehat{AED}=\widehat{ABC}+\widehat{ACB}=90^0\)
=>DE\(\perp\)AM