Lim x->2 \(\frac{\sqrt{4x+1}-3}{x^2-4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hôm trước thầy có ghi kết quả của trọng tâm tứ diện nên mình lấy kết quả đó để chứng minh luôn nhá
Gọi G là trọng tâm tứ diện. G chỉ được gọi là trọng tâm tứ diện <=> thỏa mãn 2 điều kiện sau:
1. \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\) ( hoàn toàn tương tự với vecto trọng tâm tác giác ta đã được học ở lớp 10 )
2. \(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}=4\overrightarrow{PG}\) ( với mọi P )
Gọi M và N lần lượt là trung điểm của AB và CD ( tự vẽ hình không khó đâu t vẽ ở olm thì nó mất time )
1. Ta có: \(\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GM}\)
\(\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GN}\)
Tương đương: \(2\left(\overrightarrow{GM}+\overrightarrow{GN}\right)=\overrightarrow{0}\) hay G là trung điểm của MN
Gọi H và K lần lượt là trung điểm của BC và AD
hoàn toàn chứng minh tương tự ta cũng có G là trung điểm của HK :)

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)




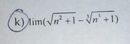
= lim x->2 \(\frac{4x+1-9}{\left(x^2-4\right)\left(\sqrt{4x+1}+3\right)}\)
= lim x->2 \(\frac{4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}\)
= lim x->2 \(\frac{4}{\left(x+2\right)\left(\sqrt{4x+1}+3\right)}\)
= lim x->2 \(\frac{4}{4.6}=\frac{4}{24}=\frac{1}{6}\)