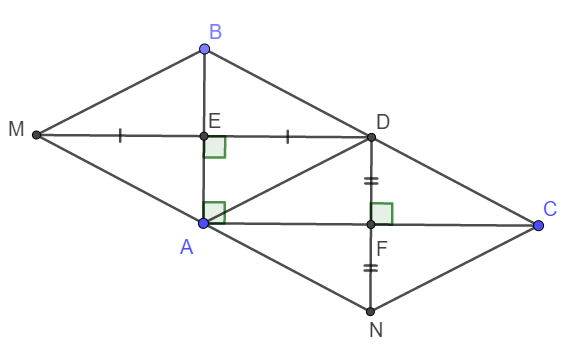
cho hình thang ABCD, AB//CD,AB=a.CB=b,DC=c,AD=d. Tia phân giác góc A, D cắt MN ở E. Tia phân giác góc tia phân giác góc B,C cắt MN tại F. M là trung điểm của AB. N là trung điêm của AC
a, M,E,F,N thẳng hàng
b, tính MN,ME thao a,b,c,d
c, Nếu a+b=c thì E trùng F