Câu 16. (2,0 điểm) Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh: tam giác ABC đồng dạng Tam giá HAC
(Chứng minh theo trường hợp cạnh-góc-cạnh)
b) Biết AB = 8(cm), BC = 10(cm) Tính độ dài HB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔACB~ΔHCA

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)(1)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔBHA có BM là phân giác
nên \(\dfrac{BH}{BA}=\dfrac{MH}{MA}\left(2\right)\)
Xét ΔBAC có BN là phân giác
nên \(\dfrac{NA}{NC}=\dfrac{BA}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{MH}{MA}=\dfrac{NA}{NC}\)
=>\(MH\cdot NC=NA\cdot MA\)

Nửa chu vi mảnh vườn là 46:2=23(m)
Gọi chiều rộng mảnh vườn là x(m)
(ĐK: x>0)
Chiều dài mảnh vườn là 23-x(m)
Chiều rộng sau khi tăng thêm 3m là x+3(m)
Chiều dài sau khi tăng thêm 2m là 23-x+2=25-x(m)
Diện tích tăng thêm 67m2 nên ta có:
(x+3)(25-x)-x(23-x)=67
=>\(25x-x^2+75-3x-23x+x^2=67\)
=>-x+75=67
=>x=75-67=8(nhận)
vậy: Chiều rộng là 8m
Chiều dài là 23-8=15m

- Mol mass của KCl: 39 +35.3 =74.5 mol/g
-Khối lượng của KCl thu được = 0,5 mol x 74.5 mol/g = 37.25 g

f=4/500
=> Tỷ lệ tần suất của biên cố E " một áo của nhà máy n không sản xuất đạt chât lượng" là 0.008.
Điều này có nghĩa là ước lượng xác suất để một chiếc áo bất kỳ từ nhà máy N không đạt chất lượng là 0.8% (tương đương với 0.008 trong hình thức thập phân)

a) Hàm số trên có:
a = -3
b = -2
Đồ thị của hàm số cắt trục tung tại điểm (0; b) nên có tung độ là -2
b) Bảng giá trị:
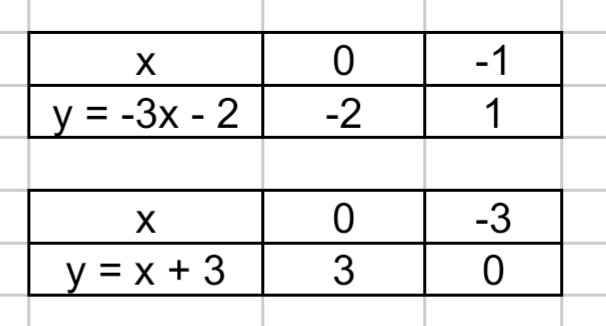
Đồ thị:
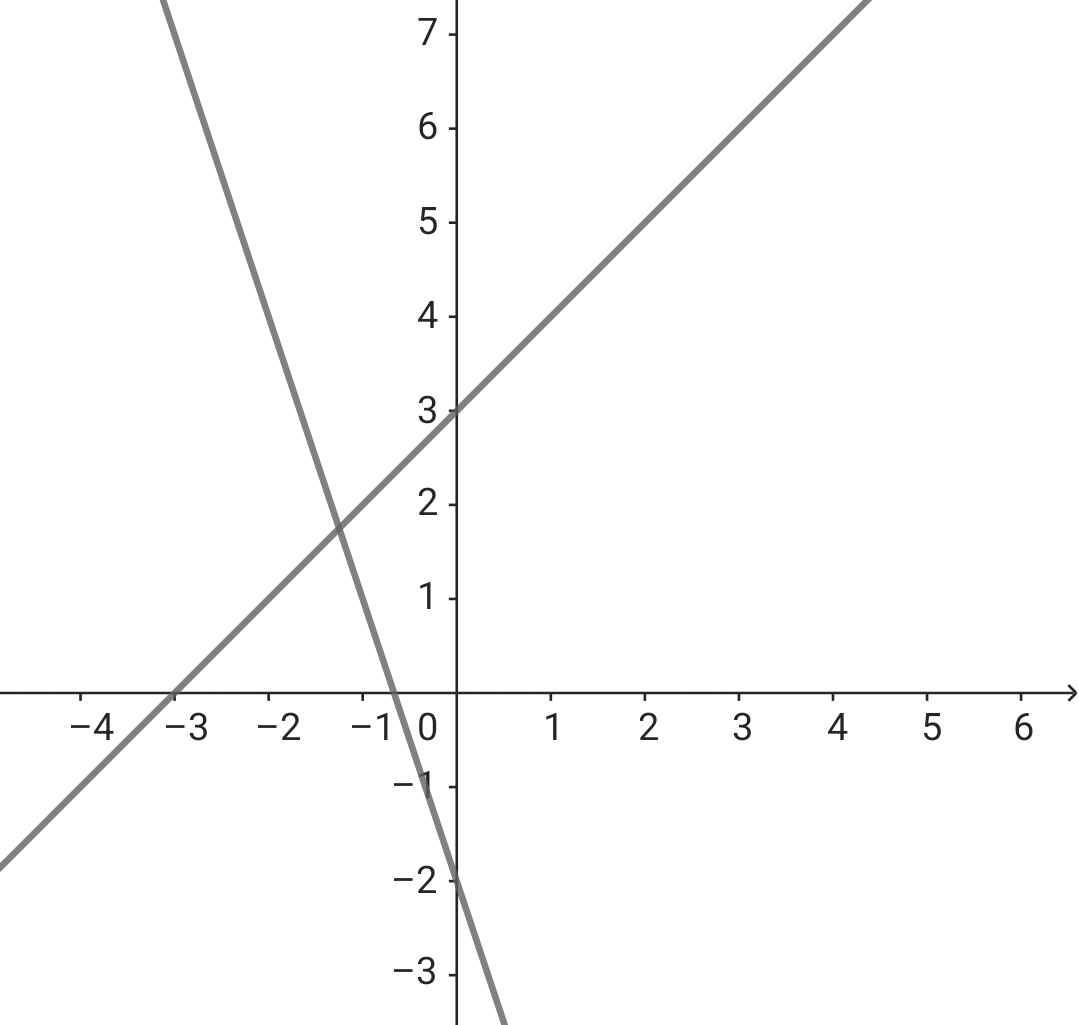
d) Phương trình hoành độ giao điểm của (d) và (d'):
-3x - 2 = x + 3
-3x - x = 3 + 2
-4x = 5
x = -5/4
y = -5/4 + 3 = 7/4
Vậy tọa độ giao điểm của (d) và (d') là (-5/4; 7/4)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó; ΔHBA~ΔABC
=>\(\dfrac{HB}{AB}=\dfrac{BA}{BC}=\dfrac{HA}{AC}\)
\(\dfrac{BA}{BC}=\dfrac{HA}{AC}\)
=>\(\dfrac{BA}{HA}=\dfrac{BC}{AC}\)
Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\dfrac{BA}{HA}=\dfrac{BC}{AC}\)
\(\widehat{ABC}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔABC~ΔHAC
b: \(\dfrac{HB}{AB}=\dfrac{BA}{BC}\)
=>\(HB=\dfrac{BA^2}{BC}=\dfrac{8^2}{10}=6,4\left(cm\right)\)