Trên quãng đường AB dài 200km có hai oto chuyển động ngược chiều. Xe thứ nhất đi từ A tới B; xe thứ hai đi từ B tới A. Nếu cùng khởi hành thì sau 2h chúng gặp nhau. Nếu xe thứ nhất khởi hành trước xe kia 2h thì hai xe gặp nhau khi xe thứ 2 đi đc 1h. Tính vận tốc mỗi xe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hàm số \(y=\left(m-2\right)^2x\) có \(a=\left(m-2\right)^2\)
Để hàm số đồng biến khi \(x>0\) thì:
\(a>0\)
\(\Rightarrow\left(m-2\right)^2>0\)
Mà: \(\left(m-2\right)^2\ge0\forall m\)
\(\Leftrightarrow\left(m-2\right)^2\ne0\)
\(\Leftrightarrow m-2\ne0\)
\(\Leftrightarrow m\ne2\)
Vậy: ...

a: 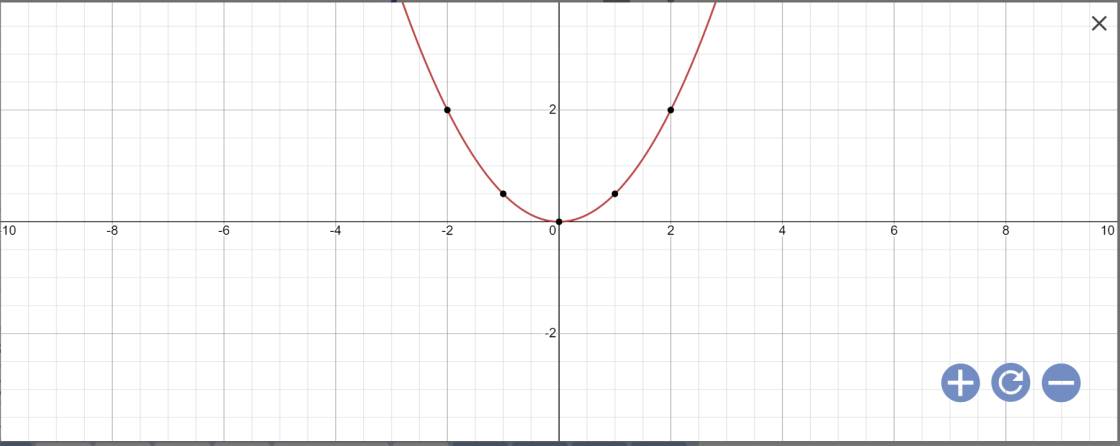
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=2x-2\)
=>\(\dfrac{1}{2}x^2-2x+2=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot\dfrac{1}{2}\cdot2=4-4=0\)
=>(P) tiếp xúc với (d) tại điểm có hoành độ là: \(x=\dfrac{-\left(-2\right)}{2\cdot\dfrac{1}{2}}=2\)
Khi x=2 thì \(y=2\cdot2-2=2\)
Vậy: (d) giao (P) tại A(2;2)

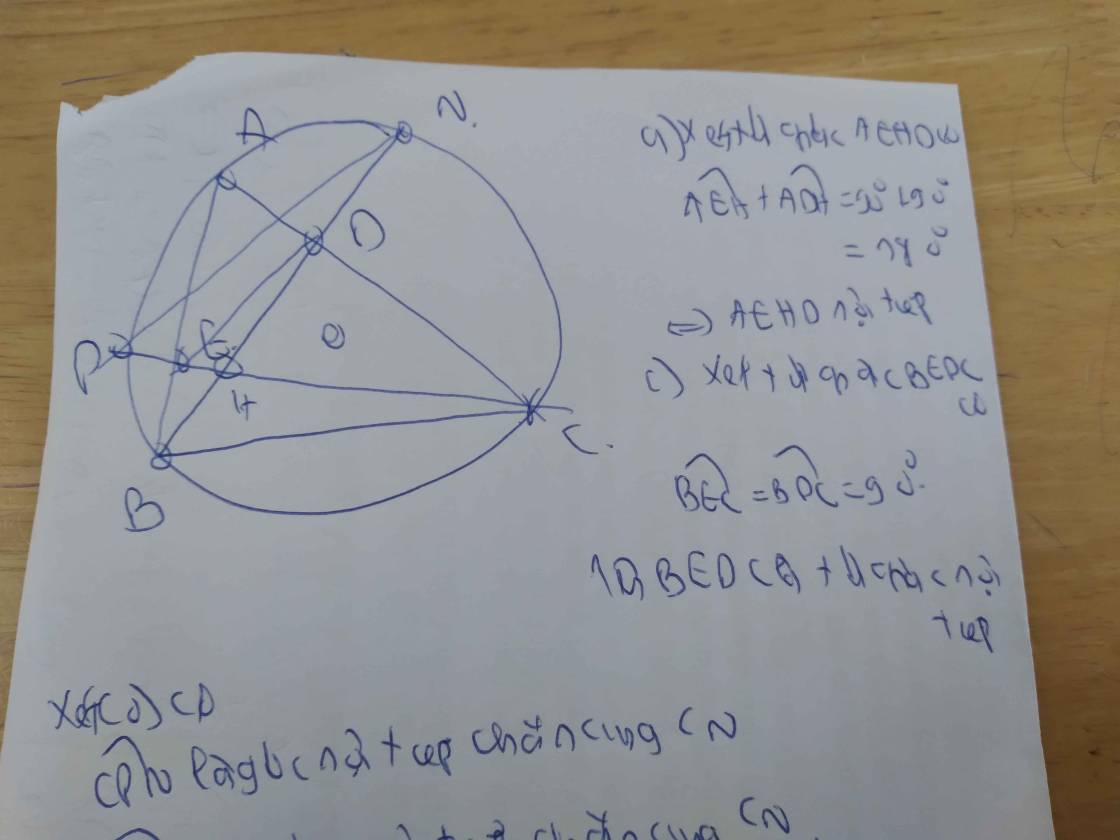
1: Xét tứ giác BCEF có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BCEF là tứ giác nội tiếp
2: Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó; ΔACK vuông tại C
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AKC}\)
Xét ΔADB vuông tại D và ΔACK vuông tại C có
\(\widehat{ABD}=\widehat{AKC}\)
Do đó: ΔADB~ΔACK
=>\(\widehat{DAB}=\widehat{CAK}\)

a: Khi m=2 thì phương trình sẽ trở thành:
\(x^2-\left(4\cdot2-1\right)x+3\cdot2^2-2\cdot2=0\)
=>\(x^2-7x+8=0\)
=>\(x^2-2\cdot x\cdot\dfrac{7}{2}+\dfrac{49}{4}-\dfrac{17}{4}=0\)
=>\(\left(x-\dfrac{7}{2}\right)^2=\dfrac{17}{4}\)
=>\(x-\dfrac{7}{2}=\pm\dfrac{\sqrt{17}}{2}\)
=>\(x=\dfrac{7}{2}\pm\dfrac{\sqrt{17}}{2}\)
b: \(\text{Δ}=\left(4m-1\right)^2-4\left(3m^2-2m\right)\)
\(=16m^2-8m+1-12m^2+8m\)
\(=4m^2+1>=1>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4m-1\\x_1x_2=\dfrac{c}{a}=3m^2-2m\end{matrix}\right.\)
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}-\dfrac{\left(x_1+x_2\right)-2}{x_1x_2}=-2\)
=>\(\dfrac{x_1+x_2}{x_1x_2}-\dfrac{\left(x_1+x_2\right)-2}{x_1x_2}=-2\)
=>\(\dfrac{2}{x_1x_2}-2\)
=>3m^2-2m=-1
=>\(3m^2-2m+1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot3\cdot1=4-12=-8< 0\)
=>\(m\in\varnothing\)

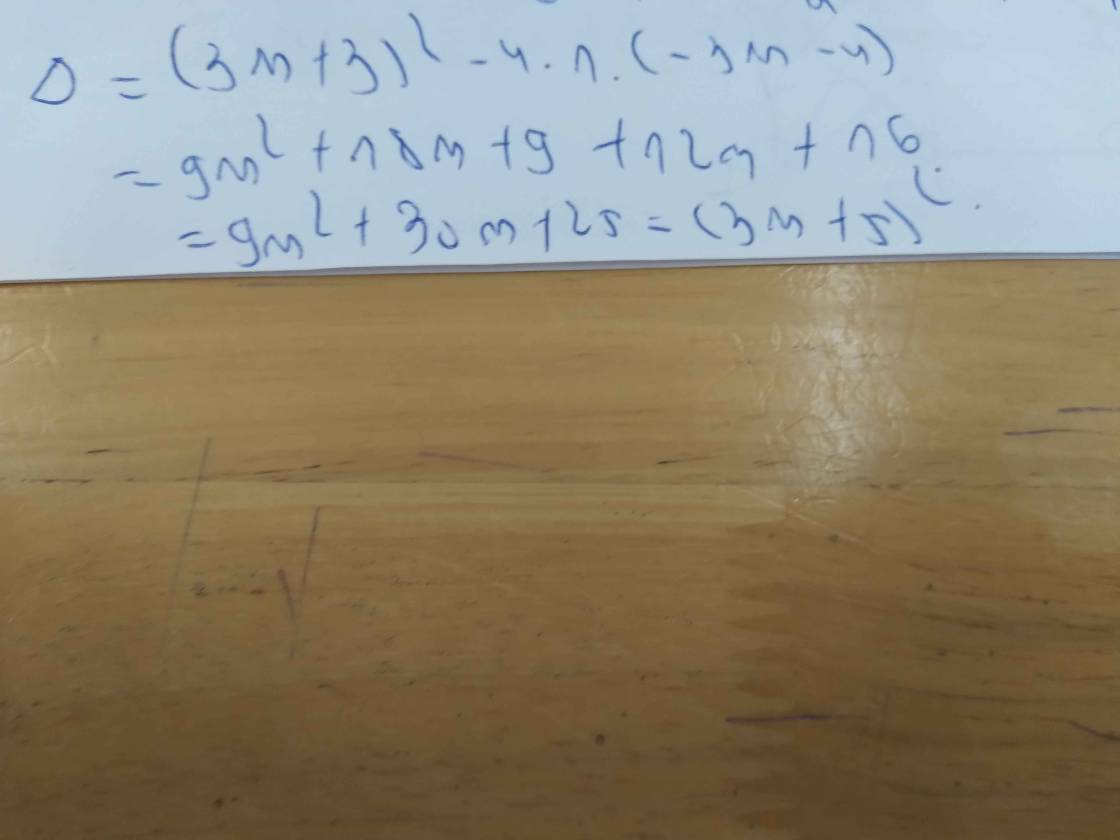
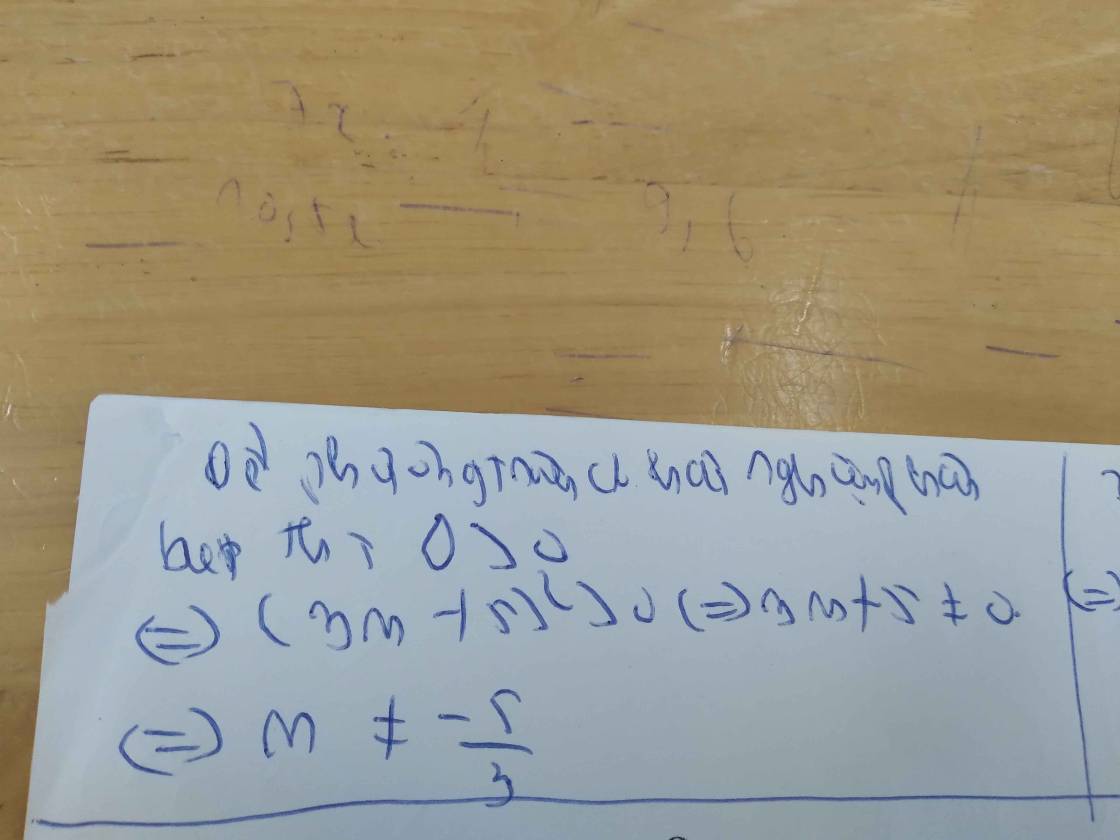

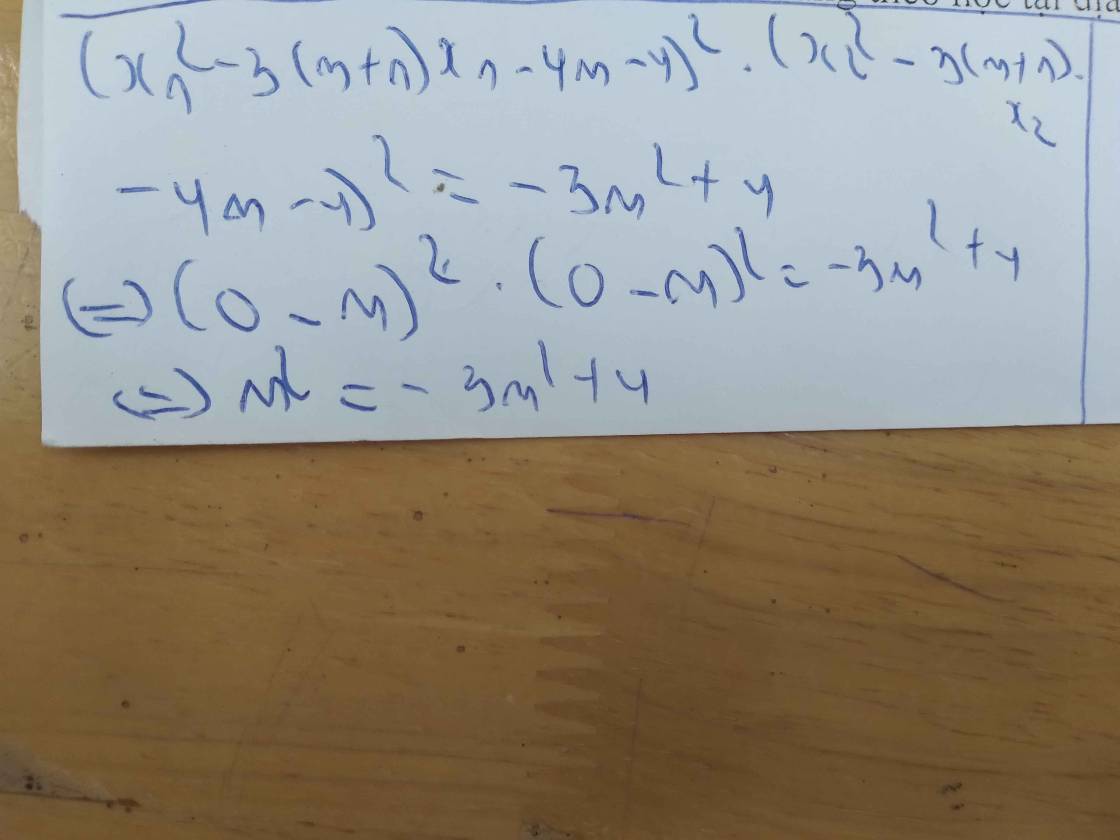
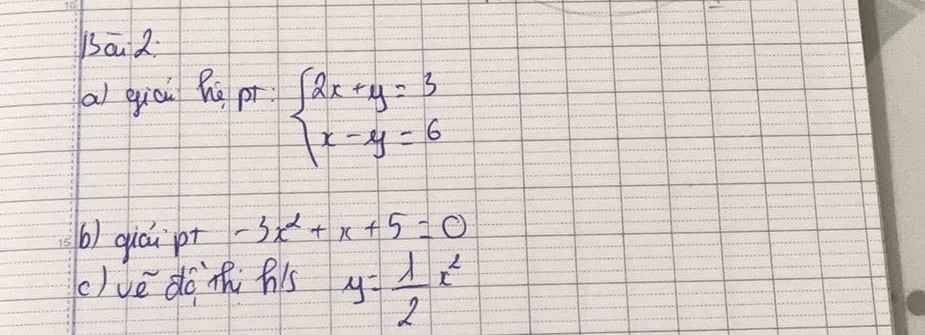




Gọi vận tốc của xe khời hành từ A là: \(x\left(km/h\right)\)
vận tốc của xe khời hành từ B là: \(y\left(km/h\right)\)
ĐK: \(x,y>0\)
Nếu khởi hành cùng lúc thì gặp nhau sau 2 giờ nên ta có pt:
\(2\left(x+y\right)=200\Leftrightarrow x+y=100\left(1\right)\)
Nếu xe thứ nhất khởi hành trước xe thứ hai 2 giờ thì hai xe gặp nhau khi xe thứ hai đi được 1 giờ
Lúc đó xe thứ 2 đã đi được: \(y\cdot1=y\left(km\right)\)
Lúc đó quãng đường mà xe thứ nhất đi được: \(\left(2+1\right)x=3x\left(km\right)\)
Ta có pt: \(3x+y=200\left(2\right)\)
Từ (1) và (2) ta có pt: \(\left\{{}\begin{matrix}x+y=100\\3x+y=200\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=100\\x+y=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=50\\y=50\end{matrix}\right.\left(tm\right)\)
Vậy: ...
Gọi vận tốc của xe 1 là x ( km/h )( x ≠0≠0)
Vận tốc của xe 2 là x + 10 ( km/h )
Quãng đường xe 1 đi được trong 2h là 2x ( km)
Quãng đường xe 2 đi được trong 2h là 2( x + 10 ) ( km )
Do hai xe này xuất phát ngược chiều nhau trên cùng một quãng đường AB dài 200 km nên ta có phương trình :
2x + 2( x + 10 ) = 200
<=> 2(x + x + 10 ) = 200
<=> 2x + 10 = 100
<=> 2x = 90
<=> x = 45
Vậy vận tốc của xe thứ hai là 45 + 10 = 55 ( km/h )
Đáp số: Xe 1: 45 km/h
Xe 2 : 55 km/h