người ta quét sơn mặt ngoài của một cái thùng không có nắp dạng hình hộp chữ nhật có chiều dài 2,5m,chiều rộng 1,5m,chiều cao 1,5m.Biêt tiền công quét sơn mỗi mét vuông là 30 000 đồng.Tính tiền công quét sơn mặt ngoài của thùng đó ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hoành độ giao điểm (P) ; (d) tm pt
\(\frac{1}{2}x^2-x-\frac{1}{2}m^2-m-1=0\)
\(\Leftrightarrow x^2-2x-m^2-2m-2=0\)
\(\Delta'=1-\left(-m^2-2m-2\right)=m^2+2m+3=\left(m+1\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb
Theo Vi et \(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=-m^2-2m-2\end{cases}}\)
Ta có \(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=68\)
\(\Leftrightarrow8-6\left(-m^2-2m-2\right)=68\)
\(\Leftrightarrow6m^2+12m-48=0\Leftrightarrow m=2;m=-4\)
Xét Pt hoành độ.......
\(\dfrac{1}{2}x^2=x+\dfrac{1}{2}m^2+m+1\\ \Leftrightarrow x^2-2x-m^2-2m-2=0\left(1\right)\)
Để ... thì Δ'>0
1+m2+2m+2>0 ⇔(m+1)2+2>0 (Hiển nhiên)
Với mọi m thì (1) sẽ có 2 nghiệm x1; x2.
*) Theo Hệ thức Viet ta có:
S=x1+x2=2 và P=x1x2= -m2-2m-2
*)Ta có:
\(\text{x^3_1 +x ^3_2 =68\Leftrightarrow(x_1+x_2)(x_1}^2-x_1x_2+x_2^2\left(\right)=68\\ \)
⇔(x1+x2)[(x1+x2)2-2x1x2-x1x2 ]=68 ⇔2[22-3(-m2-2m-2)]=68
⇔3m2+6m-24=0⇔m=2 và m=-4
KL:



\(A=\frac{3x+2}{x-3}=\frac{3\left(x-3\right)+11}{x-3}=\frac{3\left(x-3\right)}{x-3}+\frac{11}{x-3}=3+\frac{11}{x-3}\left(ĐK:x\ne3\right)\)
Để A nguyên thì \(11⋮x-3\)hay \(x-3\inƯ\left(11\right)\)
| Ư(11) | x - 3 | x |
| 1 | 1 | 4 |
| -1 | -1 | 2 |
| 11 | 11 | 14 |
| -11 | -11 | -8 |
Vậy để A nguyên \(x\in\left\{4;2;14;-8\right\}\)

Đổi: 4 giờ 30 phút = 4,5 giờ.
Ô tô đi được trong mỗi giờ là:
135 : 3 = 45 (km).
Xe máy đi được trong mỗi giờ là:
135 : 4,5 = 30 (km).
Mỗi giờ ô tô đi được nhiều hơn xe máy là:
45 - 30 = 15 ( km)
Đáp số: 15km
mỗi giờ ô tô đi được quãng đường là : \(135:3=45km\)
Đổi 4 giờ 30 phút = 4.5 giờ
Mỗi giờ xe máy đi được quãng đường là : \(135:4.5=30km\)
Vậy mỗi giờ ô tô đi được nhiều hơn xe máy là : \(45-30=15km\)


Để hai đường thẳng song song mà không trùng nhau thì điều kiện cần và đủ là :
\(\hept{\begin{cases}m=1\\3m+2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\m\ne-\frac{1}{3}\end{cases}\Leftrightarrow}m=1}\)


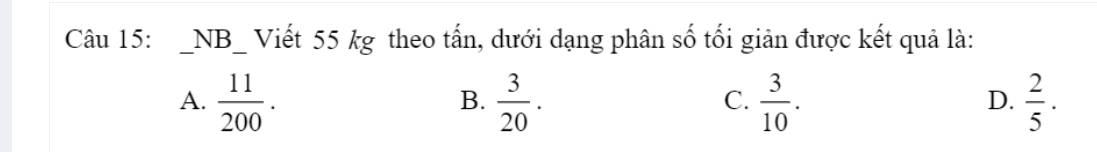 giúp mik với mik cần gấp ạ
giúp mik với mik cần gấp ạ