mình chỉ cần câu d thôi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


17 tháng 3 2022
N: là tập hợp số tự nhiên gồm các số như 0, 1, 2, 3, 4, .....
Z là tập hợp các số nguyên dương và nguyên âm như: .....-2, -1, 0, 1, 2, ....
Q là tập hợp số hữu tỉ bao gồm số nguyên dương, nguyên âm, phân số, số thập phân như: 1/2; -3; 4; 0,5; ......
Như vậy ta có thể làm bài trên như sau:
-5 thuộc N; -5 thuộc Z; - 5 thuộc Q
-3/7 không thuộc Z; -3/7 thuộc Q; N thuộc Q.
PT
1

18 tháng 3 2022
số hs giỏi của lớp là:
\(45.15\%=6,75\left(???\right)\)HS bị lẻ tính kiểu zề:>
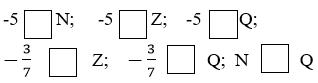
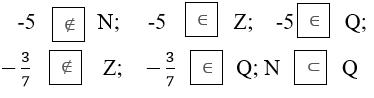

a.Dấu hiệu là điểm kiểm tra môn toán học kì 1 của 32 học sinh lớp 7
b.Để lập bảng tần số, con kẻ 2 cột:
B1: cột 1 có tên là giá trị (x), cột 2 có tên là tần số (n)
B2: Viết các giá trị từ nhỏ đến lớn vào cột 1
B3: Đếm số lần giá trị xuất hiện ghi vào cột 2